Menu Close

calculate-f-a-0-cos-sh-2x-x-2-a-2-dx-and-g-a-0-cos-sh-2x-x-2-a-2-2-a-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 96198 by mathmax by abdo last updated on 30/May/20
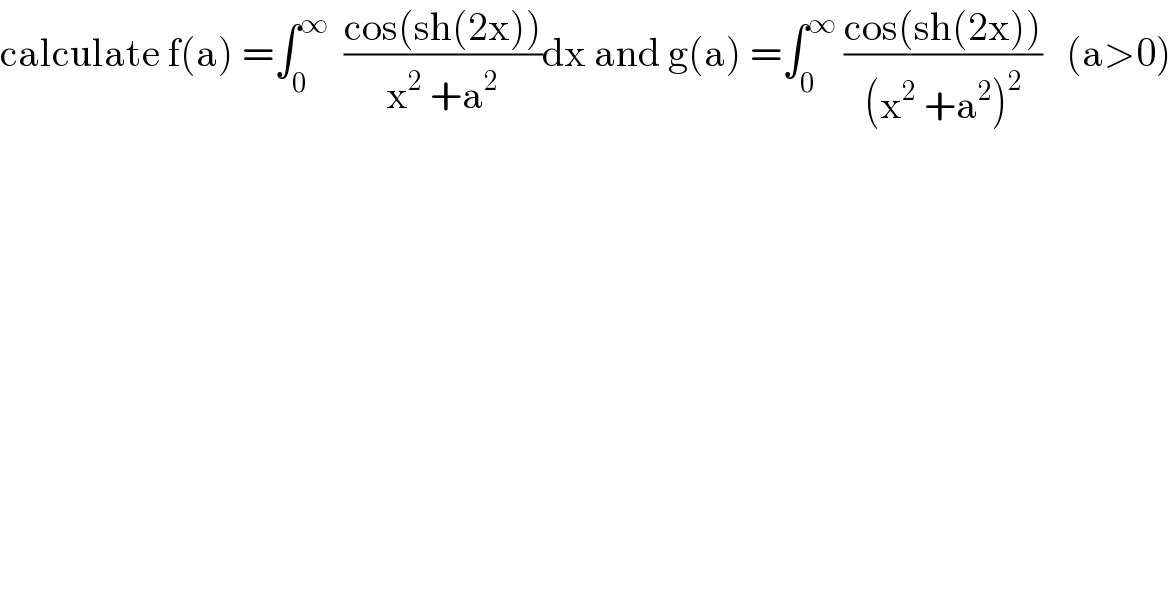
calculate f(a) =∫_0 ^∞ ((cos(sh(2x)))/(x^2 +a^2 ))dx and g(a) =∫_0 ^∞ ((cos(sh(2x)))/((x^2 +a^2 )^2 )) (a>0)
$$\mathrm{calculate}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{and}\:\mathrm{g}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\:\left(\mathrm{a}>\mathrm{0}\right) \\ $$
Answered by mathmax by abdo last updated on 01/Jun/20
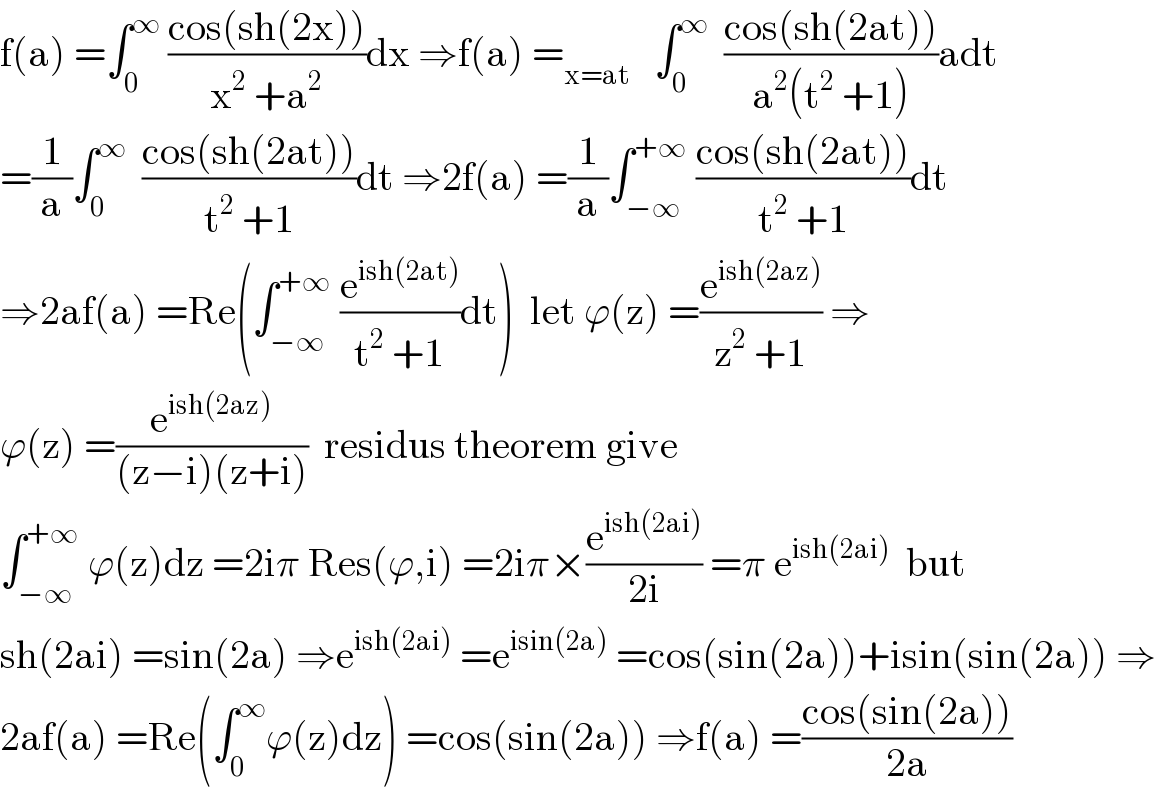
f(a) =∫_0 ^∞ ((cos(sh(2x)))/(x^2 +a^2 ))dx ⇒f(a) =_(x=at) ∫_0 ^∞ ((cos(sh(2at)))/(a^2 (t^2 +1)))adt =(1/a)∫_0 ^∞ ((cos(sh(2at)))/(t^2 +1))dt ⇒2f(a) =(1/a)∫_(−∞) ^(+∞) ((cos(sh(2at)))/(t^2 +1))dt ⇒2af(a) =Re(∫_(−∞) ^(+∞) (e^(ish(2at)) /(t^2 +1))dt) let ϕ(z) =(e^(ish(2az)) /(z^2 +1)) ⇒ ϕ(z) =(e^(ish(2az)) /((z−i)(z+i))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) =2iπ×(e^(ish(2ai)) /(2i)) =π e^(ish(2ai)) but sh(2ai) =sin(2a) ⇒e^(ish(2ai)) =e^(isin(2a)) =cos(sin(2a))+isin(sin(2a)) ⇒ 2af(a) =Re(∫_0 ^∞ ϕ(z)dz) =cos(sin(2a)) ⇒f(a) =((cos(sin(2a)))/(2a))
$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=_{\mathrm{x}=\mathrm{at}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2at}\right)\right)}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{adt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2at}\right)\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:\Rightarrow\mathrm{2f}\left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2at}\right)\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$\Rightarrow\mathrm{2af}\left(\mathrm{a}\right)\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{ish}\left(\mathrm{2at}\right)} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right)\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{ish}\left(\mathrm{2az}\right)} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{ish}\left(\mathrm{2az}\right)} }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{2i}\pi×\frac{\mathrm{e}^{\mathrm{ish}\left(\mathrm{2ai}\right)} }{\mathrm{2i}}\:=\pi\:\mathrm{e}^{\mathrm{ish}\left(\mathrm{2ai}\right)} \:\:\mathrm{but} \\ $$$$\mathrm{sh}\left(\mathrm{2ai}\right)\:=\mathrm{sin}\left(\mathrm{2a}\right)\:\Rightarrow\mathrm{e}^{\mathrm{ish}\left(\mathrm{2ai}\right)} \:=\mathrm{e}^{\mathrm{isin}\left(\mathrm{2a}\right)} \:=\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)+\mathrm{isin}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)\:\Rightarrow \\ $$$$\mathrm{2af}\left(\mathrm{a}\right)\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\right)\:=\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)}{\mathrm{2a}} \\ $$
Commented by mathmax by abdo last updated on 01/Jun/20
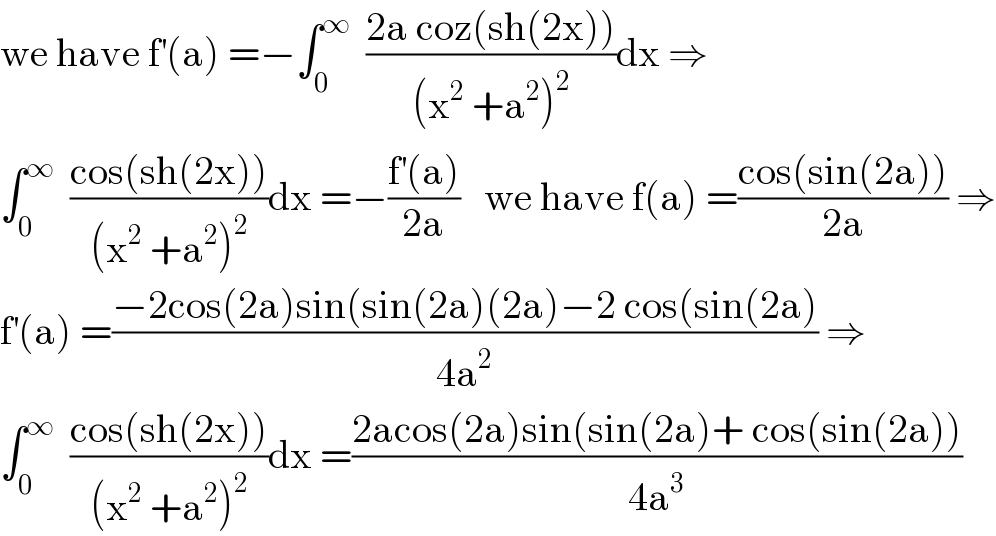
we have f^′ (a) =−∫_0 ^∞ ((2a coz(sh(2x)))/((x^2 +a^2 )^2 ))dx ⇒ ∫_0 ^∞ ((cos(sh(2x)))/((x^2 +a^2 )^2 ))dx =−((f^′ (a))/(2a)) we have f(a) =((cos(sin(2a)))/(2a)) ⇒ f^′ (a) =((−2cos(2a)sin(sin(2a)(2a)−2 cos(sin(2a))/(4a^2 )) ⇒ ∫_0 ^∞ ((cos(sh(2x)))/((x^2 +a^2 )^2 ))dx =((2acos(2a)sin(sin(2a)+ cos(sin(2a)))/(4a^3 ))
$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2a}\:\mathrm{coz}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=−\frac{\mathrm{f}^{'} \left(\mathrm{a}\right)}{\mathrm{2a}}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)}{\mathrm{2a}}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{−\mathrm{2cos}\left(\mathrm{2a}\right)\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{2a}\right)\left(\mathrm{2a}\right)−\mathrm{2}\:\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right.\right.}{\mathrm{4a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\frac{\mathrm{2acos}\left(\mathrm{2a}\right)\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{2a}\right)+\:\mathrm{cos}\left(\mathrm{sin}\left(\mathrm{2a}\right)\right)\right.}{\mathrm{4a}^{\mathrm{3}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *