Menu Close

calculate-f-a-0-e-x-2-a-x-2-dx-with-a-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 79107 by mathmax by abdo last updated on 22/Jan/20
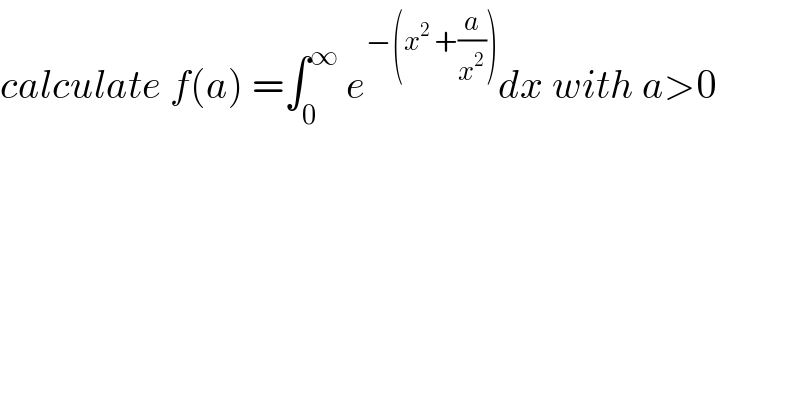
calculate f(a) =∫_0 ^∞ e^(−(x^2 +(a/x^2 ))) dx with a>0
$${calculate}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({x}^{\mathrm{2}} \:+\frac{{a}}{{x}^{\mathrm{2}} }\right)} {dx}\:{with}\:{a}>\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 23/Jan/20
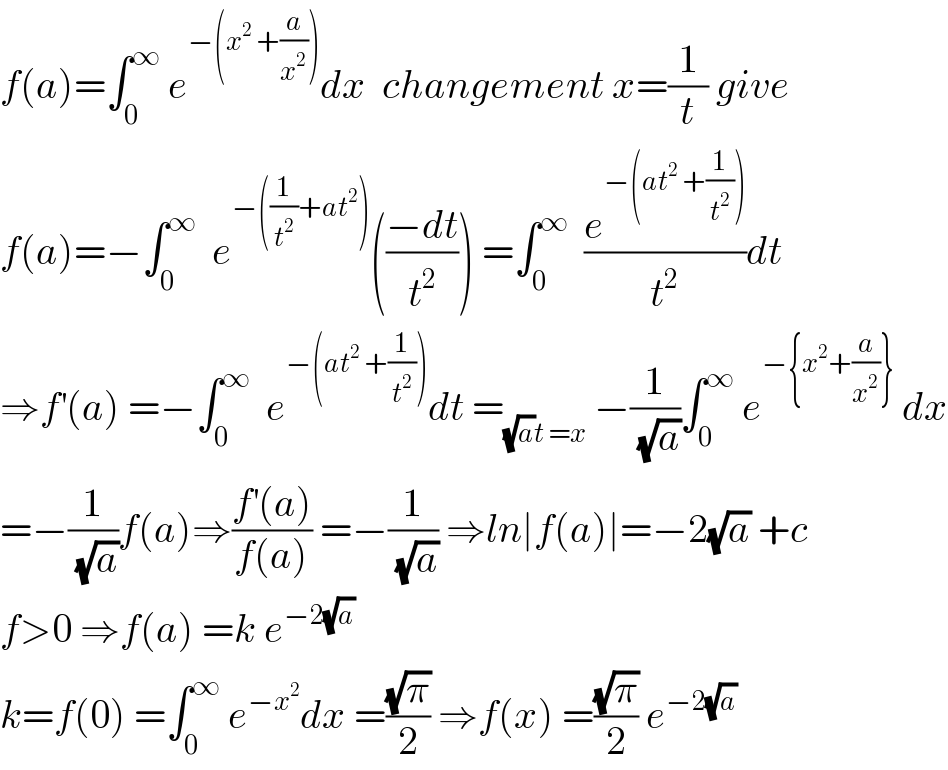
f(a)=∫_0 ^∞ e^(−(x^2 +(a/x^2 ))) dx changement x=(1/t) give f(a)=−∫_0 ^∞ e^(−((1/t^2 )+at^2 )) (((−dt)/t^2 )) =∫_0 ^∞ (e^(−(at^2 +(1/t^2 ))) /t^2 )dt ⇒f^′ (a) =−∫_0 ^∞ e^(−(at^2 +(1/t^2 ))) dt =_((√a)t =x) −(1/( (√a)))∫_0 ^∞ e^(−{x^2 +(a/x^2 )}) dx =−(1/( (√a)))f(a)⇒((f^′ (a))/(f(a))) =−(1/( (√a))) ⇒ln∣f(a)∣=−2(√a) +c f>0 ⇒f(a) =k e^(−2(√a)) k=f(0) =∫_0 ^∞ e^(−x^2 ) dx =((√π)/2) ⇒f(x) =((√π)/2) e^(−2(√a))
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({x}^{\mathrm{2}} \:+\frac{{a}}{{x}^{\mathrm{2}} }\right)} {dx}\:\:{changement}\:{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$${f}\left({a}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+{at}^{\mathrm{2}} \right)} \left(\frac{−{dt}}{{t}^{\mathrm{2}} }\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left({at}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)} }{{t}^{\mathrm{2}} }{dt} \\ $$$$\Rightarrow{f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({at}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)} {dt}\:=_{\sqrt{{a}}{t}\:={x}} \:−\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left\{{x}^{\mathrm{2}} +\frac{{a}}{{x}^{\mathrm{2}} }\right\}} \:{dx} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{{a}}}{f}\left({a}\right)\Rightarrow\frac{{f}^{'} \left({a}\right)}{{f}\left({a}\right)}\:=−\frac{\mathrm{1}}{\:\sqrt{{a}}}\:\Rightarrow{ln}\mid{f}\left({a}\right)\mid=−\mathrm{2}\sqrt{{a}}\:+{c} \\ $$$${f}>\mathrm{0}\:\Rightarrow{f}\left({a}\right)\:={k}\:{e}^{−\mathrm{2}\sqrt{{a}}} \\ $$$${k}={f}\left(\mathrm{0}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{−\mathrm{2}\sqrt{{a}}} \\ $$
Answered by ~blr237~ last updated on 22/Jan/20
let state u=(1/x) then dx=−(du/u^2 ) f(a)=∫_0 ^∞ e^(−((1/u^2 )+au^2 )) (du/u^2 ) f∈C^(1 ) cause for all a>0 ∣e^(−(x^2 +(a/x^2 ))) ∣≤e^(−x^2 ) and ∫_(0 ) ^∞ e^(−x^2 ) dx=((√π)/2) so converges Now we can write (df/da)=−∫_0 ^∞ e^(−(au^2 +(1/u^2 ))) du =−(1/( (√a)))∫_0 ^∞ e^(−[(u(√a))^2 +(a/((u(√a))^2 ))]) d(u(√a)) =−(1/( (√a))) ∫_(0 ) ^∞ e^(−(v^2 +(a/v^2 ))) dv with v=u(√a) So (df/da)=−(1/( (√a))) f(a) Then ln∣f(a)∣=−2(√a) +c ⇒f(a)=ke^(−2(√a)) with k>0 we know that lim_(a→0) f(a)=k=((√π)/2) Finaly f(a)=((√π)/2) e^(−2(√a))
$${let}\:{state}\:{u}=\frac{\mathrm{1}}{{x}}\:\:{then}\:{dx}=−\frac{{du}}{{u}^{\mathrm{2}} }\: \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} }+{au}^{\mathrm{2}} \right)} \frac{{du}}{{u}^{\mathrm{2}} }\: \\ $$$${f}\in{C}^{\mathrm{1}\:} \:{cause}\:{for}\:{all}\:{a}>\mathrm{0}\:\mid{e}^{−\left({x}^{\mathrm{2}} +\frac{{a}}{{x}^{\mathrm{2}} }\right)} \mid\leqslant{e}^{−{x}^{\mathrm{2}} } \:\:{and}\:\int_{\mathrm{0}\:} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\:\:{so}\:{converges} \\ $$$${Now}\:{we}\:{can}\:{write}\: \\ $$$$\frac{{df}}{{da}}=−\int_{\mathrm{0}} ^{\infty} {e}^{−\left({au}^{\mathrm{2}} +\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right)} {du} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} {e}^{−\left[\left({u}\sqrt{{a}}\right)^{\mathrm{2}} +\frac{{a}}{\left({u}\sqrt{{a}}\right)^{\mathrm{2}} }\right]} {d}\left({u}\sqrt{{a}}\right) \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\:\sqrt{{a}}}\:\int_{\mathrm{0}\:} ^{\infty} {e}^{−\left({v}^{\mathrm{2}} +\frac{{a}}{{v}^{\mathrm{2}} }\right)} {dv}\:\:\:\:\:{with}\:{v}={u}\sqrt{{a}}\: \\ $$$$\:\:\:{So}\:\:\:\frac{{df}}{{da}}=−\frac{\mathrm{1}}{\:\sqrt{{a}}}\:{f}\left({a}\right) \\ $$$${Then}\:\:{ln}\mid{f}\left({a}\right)\mid=−\mathrm{2}\sqrt{{a}}\:+{c}\:\Rightarrow{f}\left({a}\right)={ke}^{−\mathrm{2}\sqrt{{a}}} \:\:{with}\:{k}>\mathrm{0} \\ $$$${we}\:{know}\:{that}\:\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({a}\right)={k}=\frac{\sqrt{\pi}}{\mathrm{2}}\: \\ $$$${Finaly}\:\:\:\:{f}\left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{−\mathrm{2}\sqrt{{a}}} \: \\ $$$$ \\ $$$$ \\ $$
Commented by msup trace by abdo last updated on 22/Jan/20
thanks sir
$${thanks}\:{sir} \\ $$
Answered by mind is power last updated on 22/Jan/20
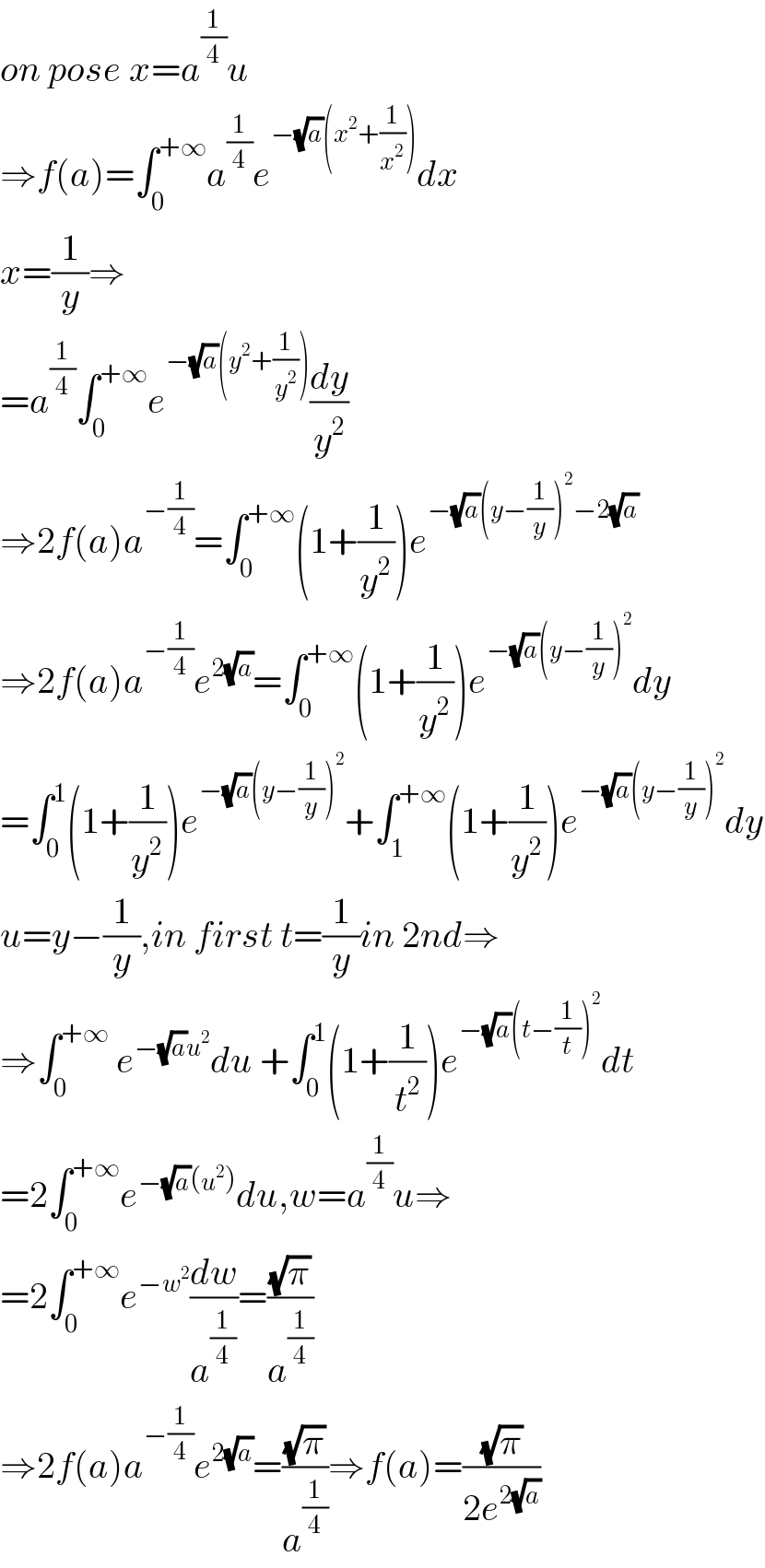
on pose x=a^(1/4) u ⇒f(a)=∫_0 ^(+∞) a^(1/4) e^(−(√a)(x^2 +(1/x^2 ))) dx x=(1/y)⇒ =a^(1/4) ∫_0 ^(+∞) e^(−(√a)(y^2 +(1/y^2 ))) (dy/y^2 ) ⇒2f(a)a^(−(1/4)) =∫_0 ^(+∞) (1+(1/y^2 ))e^(−(√a)(y−(1/y))^2 −2(√a)) ⇒2f(a)a^(−(1/4)) e^(2(√a)) =∫_0 ^(+∞) (1+(1/y^2 ))e^(−(√a)(y−(1/y))^2 ) dy =∫_0 ^1 (1+(1/y^2 ))e^(−(√a)(y−(1/y))^2 ) +∫_1 ^(+∞) (1+(1/y^2 ))e^(−(√a)(y−(1/y))^2 ) dy u=y−(1/y),in first t=(1/y)in 2nd⇒ ⇒∫_0 ^(+∞) e^(−(√a)u^2 ) du +∫_0 ^1 (1+(1/t^2 ))e^(−(√a)(t−(1/t))^2 ) dt =2∫_0 ^(+∞) e^(−(√a)(u^2 )) du,w=a^(1/4) u⇒ =2∫_0 ^(+∞) e^(−w^2 ) (dw/a^(1/4) )=((√π)/a^(1/4) ) ⇒2f(a)a^(−(1/4)) e^(2(√a)) =((√π)/a^(1/4) )⇒f(a)=((√π)/(2e^(2(√a)) ))
$${on}\:{pose}\:{x}={a}^{\frac{\mathrm{1}}{\mathrm{4}}} {u} \\ $$$$\Rightarrow{f}\left({a}\right)=\int_{\mathrm{0}} ^{+\infty} {a}^{\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\sqrt{{a}}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} {dx} \\ $$$${x}=\frac{\mathrm{1}}{{y}}\Rightarrow \\ $$$$={a}^{\frac{\mathrm{1}}{\mathrm{4}}} \int_{\mathrm{0}} ^{+\infty} {e}^{−\sqrt{{a}}\left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)} \frac{{dy}}{{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}{f}\left({a}\right){a}^{−\frac{\mathrm{1}}{\mathrm{4}}} =\int_{\mathrm{0}} ^{+\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right){e}^{−\sqrt{{a}}\left({y}−\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{{a}}} \\ $$$$\Rightarrow\mathrm{2}{f}\left({a}\right){a}^{−\frac{\mathrm{1}}{\mathrm{4}}} {e}^{\mathrm{2}\sqrt{{a}}} =\int_{\mathrm{0}} ^{+\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right){e}^{−\sqrt{{a}}\left({y}−\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} } {dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right){e}^{−\sqrt{{a}}\left({y}−\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} } +\int_{\mathrm{1}} ^{+\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right){e}^{−\sqrt{{a}}\left({y}−\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} } {dy} \\ $$$${u}={y}−\frac{\mathrm{1}}{{y}},{in}\:{first}\:{t}=\frac{\mathrm{1}}{{y}}{in}\:\mathrm{2}{nd}\Rightarrow \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \:{e}^{−\sqrt{{a}}{u}^{\mathrm{2}} } {du}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){e}^{−\sqrt{{a}}\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} } {dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {e}^{−\sqrt{{a}}\left({u}^{\mathrm{2}} \right)} {du},{w}={a}^{\frac{\mathrm{1}}{\mathrm{4}}} {u}\Rightarrow \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {e}^{−{w}^{\mathrm{2}} } \frac{{dw}}{{a}^{\frac{\mathrm{1}}{\mathrm{4}}} }=\frac{\sqrt{\pi}}{{a}^{\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$$\Rightarrow\mathrm{2}{f}\left({a}\right){a}^{−\frac{\mathrm{1}}{\mathrm{4}}} {e}^{\mathrm{2}\sqrt{{a}}} =\frac{\sqrt{\pi}}{{a}^{\frac{\mathrm{1}}{\mathrm{4}}} }\Rightarrow{f}\left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}{e}^{\mathrm{2}\sqrt{{a}}} } \\ $$
Commented by msup trace by abdo last updated on 22/Jan/20
thanks sir.
$${thanks}\:{sir}. \\ $$
Commented by mind is power last updated on 22/Jan/20
y′re welcom
$${y}'{re}\:{welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *