Menu Close

calculate-f-dx-x-2-2x-cos-1-2-calculate-g-sin-x-2-2x-cos-1-2-dx-3-find-f-n-with-n-integr-natural-4-calculate-dx

Tinku Tara 0 Comments
Pin




Question Number 47295 by maxmathsup by imad last updated on 07/Nov/18
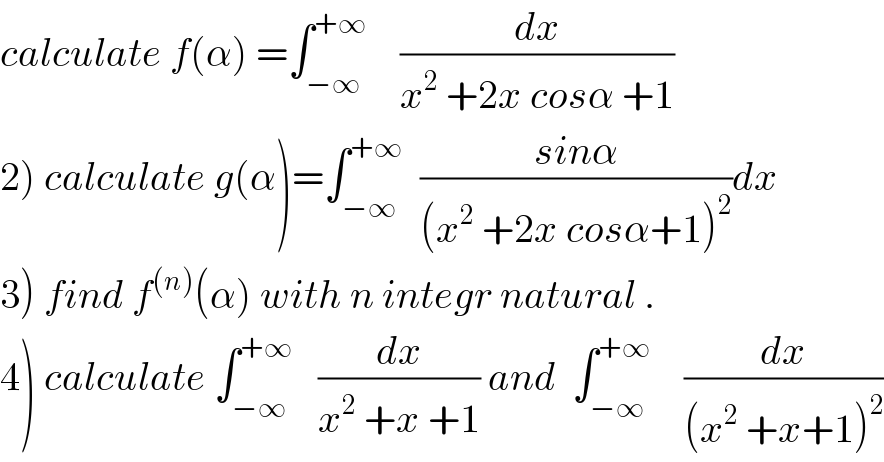
calculate f(α) =∫_(−∞) ^(+∞) (dx/(x^2 +2x cosα +1)) 2) calculate g(α)=∫_(−∞) ^(+∞) ((sinα)/((x^2 +2x cosα+1)^2 ))dx 3) find f^((n)) (α) with n integr natural . 4) calculate ∫_(−∞) ^(+∞) (dx/(x^2 +x +1)) and ∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^2 ))
$${calculate}\:{f}\left(\alpha\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\alpha\:+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{g}\left(\alpha\right)=\int_{−\infty} ^{+\infty} \:\:\frac{{sin}\alpha}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\alpha+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{f}^{\left({n}\right)} \left(\alpha\right)\:{with}\:{n}\:{integr}\:{natural}\:. \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}\:+\mathrm{1}}\:{and}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
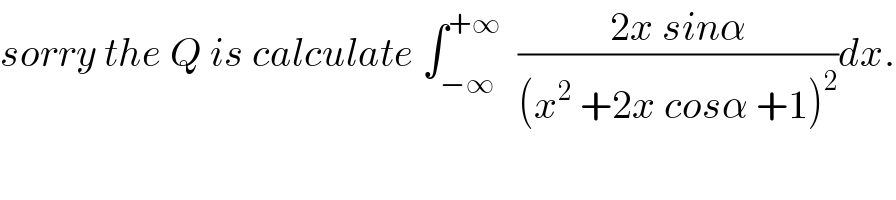
sorry the Q is calculate ∫_(−∞) ^(+∞) ((2x sinα)/((x^2 +2x cosα +1)^2 ))dx.
$${sorry}\:{the}\:{Q}\:{is}\:{calculate}\:\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{2}{x}\:{sin}\alpha}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\alpha\:+\mathrm{1}\right)^{\mathrm{2}} }{dx}. \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
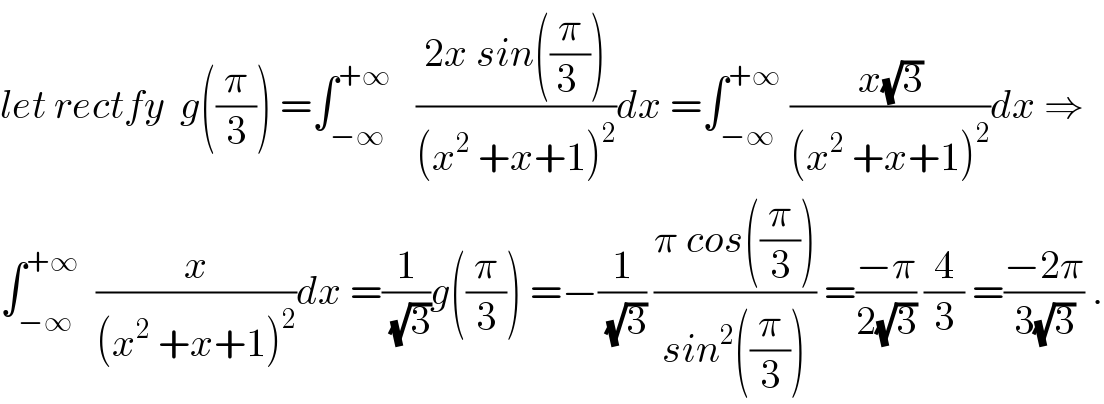
let rectfy g((π/3)) =∫_(−∞) ^(+∞) ((2x sin((π/(3 ))))/((x^2 +x+1)^2 ))dx =∫_(−∞) ^(+∞) ((x(√3))/((x^2 +x+1)^2 ))dx ⇒ ∫_(−∞) ^(+∞) (x/((x^2 +x+1)^2 ))dx =(1/( (√3)))g((π/3)) =−(1/( (√3))) ((π cos((π/3)))/(sin^2 ((π/3)))) =((−π)/(2(√3))) (4/3) =((−2π)/(3(√3))) .
$${let}\:{rectfy}\:\:{g}\left(\frac{\pi}{\mathrm{3}}\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{2}{x}\:{sin}\left(\frac{\pi}{\mathrm{3}\:}\right)}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}\sqrt{\mathrm{3}}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\frac{{x}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{g}\left(\frac{\pi}{\mathrm{3}}\right)\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\frac{\pi\:{cos}\left(\frac{\pi}{\mathrm{3}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{−\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\frac{\mathrm{4}}{\mathrm{3}}\:=\frac{−\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:. \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
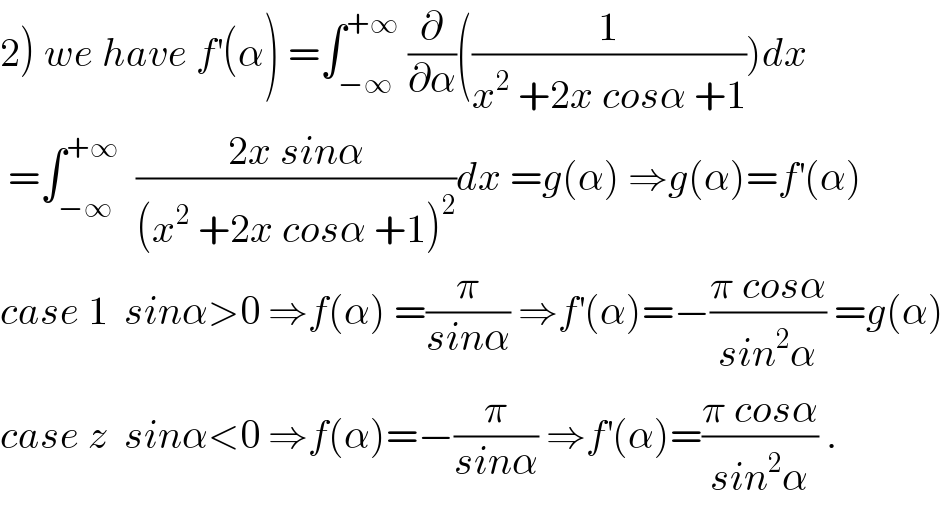
2) we have f^′ (α) =∫_(−∞) ^(+∞) (∂/∂α)((1/(x^2 +2x cosα +1)))dx =∫_(−∞) ^(+∞) ((2x sinα)/((x^2 +2x cosα +1)^2 ))dx =g(α) ⇒g(α)=f^′ (α) case 1 sinα>0 ⇒f(α) =(π/(sinα)) ⇒f^′ (α)=−((π cosα)/(sin^2 α)) =g(α) case z sinα<0 ⇒f(α)=−(π/(sinα)) ⇒f^′ (α)=((π cosα)/(sin^2 α)) .
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left(\alpha\right)\:=\int_{−\infty} ^{+\infty} \:\frac{\partial}{\partial\alpha}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\alpha\:+\mathrm{1}}\right){dx} \\ $$$$\:=\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{2}{x}\:{sin}\alpha}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\alpha\:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:={g}\left(\alpha\right)\:\Rightarrow{g}\left(\alpha\right)={f}^{'} \left(\alpha\right) \\ $$$${case}\:\mathrm{1}\:\:{sin}\alpha>\mathrm{0}\:\Rightarrow{f}\left(\alpha\right)\:=\frac{\pi}{{sin}\alpha}\:\Rightarrow{f}^{'} \left(\alpha\right)=−\frac{\pi\:{cos}\alpha}{{sin}^{\mathrm{2}} \alpha}\:={g}\left(\alpha\right) \\ $$$${case}\:{z}\:\:{sin}\alpha<\mathrm{0}\:\Rightarrow{f}\left(\alpha\right)=−\frac{\pi}{{sin}\alpha}\:\Rightarrow{f}^{'} \left(\alpha\right)=\frac{\pi\:{cos}\alpha}{{sin}^{\mathrm{2}} \alpha}\:. \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
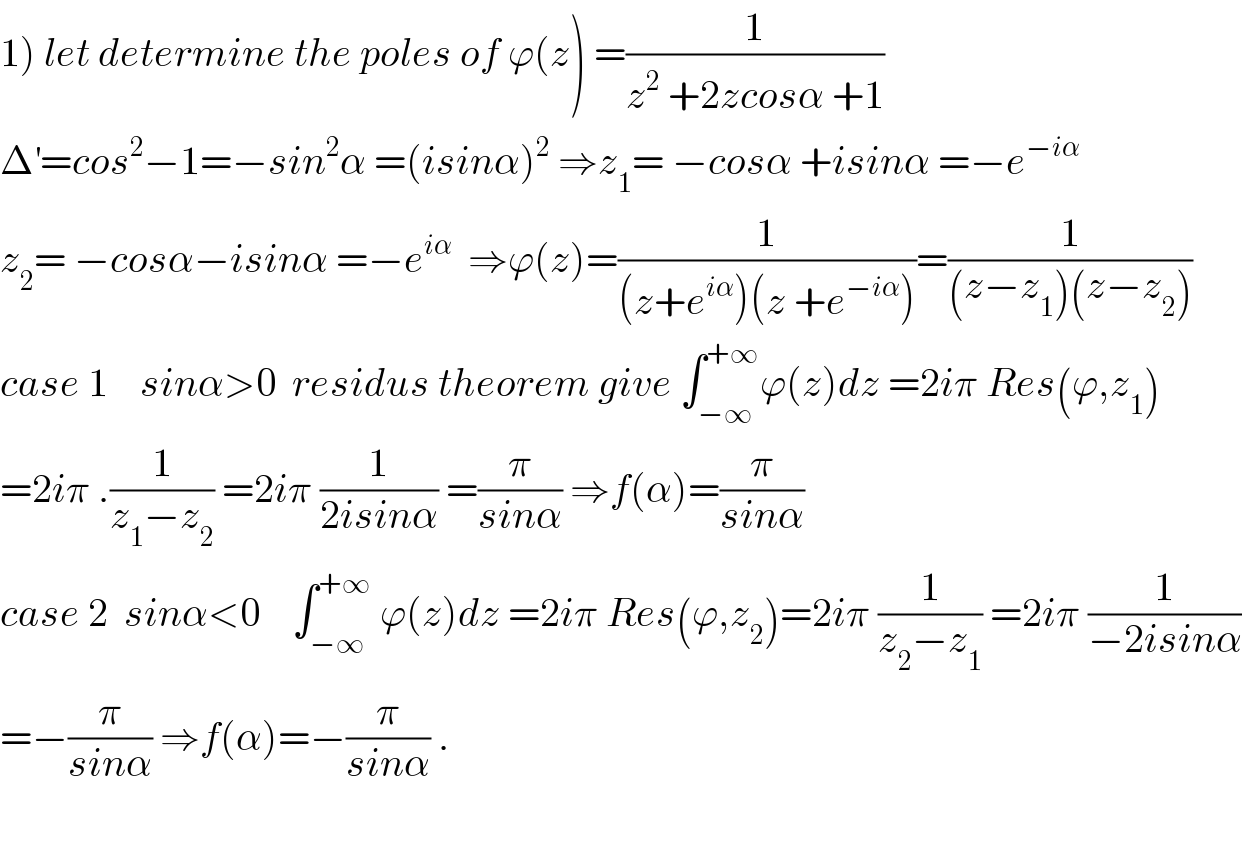
1) let determine the poles of ϕ(z) =(1/(z^2 +2zcosα +1)) Δ^′ =cos^2 −1=−sin^2 α =(isinα)^2 ⇒z_1 = −cosα +isinα =−e^(−iα) z_2 = −cosα−isinα =−e^(iα) ⇒ϕ(z)=(1/((z+e^(iα) )(z +e^(−iα) )))=(1/((z−z_1 )(z−z_2 ))) case 1 sinα>0 residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,z_1 ) =2iπ .(1/(z_1 −z_2 )) =2iπ (1/(2isinα)) =(π/(sinα)) ⇒f(α)=(π/(sinα)) case 2 sinα<0 ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,z_2 )=2iπ (1/(z_2 −z_1 )) =2iπ (1/(−2isinα)) =−(π/(sinα)) ⇒f(α)=−(π/(sinα)) .
$$\left.\mathrm{1}\right)\:{let}\:{determine}\:{the}\:{poles}\:{of}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{2}} \:+\mathrm{2}{zcos}\alpha\:+\mathrm{1}} \\ $$$$\Delta^{'} ={cos}^{\mathrm{2}} −\mathrm{1}=−{sin}^{\mathrm{2}} \alpha\:=\left({isin}\alpha\right)^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\:−{cos}\alpha\:+{isin}\alpha\:=−{e}^{−{i}\alpha} \\ $$$${z}_{\mathrm{2}} =\:−{cos}\alpha−{isin}\alpha\:=−{e}^{{i}\alpha} \:\:\Rightarrow\varphi\left({z}\right)=\frac{\mathrm{1}}{\left({z}+{e}^{{i}\alpha} \right)\left({z}\:+{e}^{−{i}\alpha} \right)}=\frac{\mathrm{1}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$${case}\:\mathrm{1}\:\:\:\:{sin}\alpha>\mathrm{0}\:\:{residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$$=\mathrm{2}{i}\pi\:.\frac{\mathrm{1}}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} }\:=\mathrm{2}{i}\pi\:\frac{\mathrm{1}}{\mathrm{2}{isin}\alpha}\:=\frac{\pi}{{sin}\alpha}\:\Rightarrow{f}\left(\alpha\right)=\frac{\pi}{{sin}\alpha} \\ $$$${case}\:\mathrm{2}\:\:{sin}\alpha<\mathrm{0}\:\:\:\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{2}} \right)=\mathrm{2}{i}\pi\:\frac{\mathrm{1}}{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\:=\mathrm{2}{i}\pi\:\frac{\mathrm{1}}{−\mathrm{2}{isin}\alpha} \\ $$$$=−\frac{\pi}{{sin}\alpha}\:\Rightarrow{f}\left(\alpha\right)=−\frac{\pi}{{sin}\alpha}\:. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
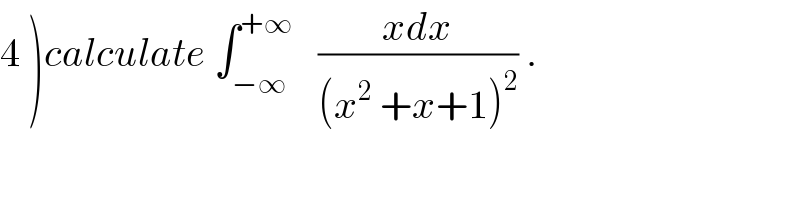
4 )calculate ∫_(−∞) ^(+∞) ((xdx)/((x^2 +x+1)^2 )) .
$$\left.\mathrm{4}\:\right){calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{xdx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$
Commented by maxmathsup by imad last updated on 08/Nov/18
4) ★we have x^2 +x +1 =x^2 +2(1/2)x +1 =x^2 +2x cos((π/3))+1 ⇒ ∫_(−∞) ^(+∞) (dx/(x^2 +x+1)) =f((π/3)) =(π/(sin((π/3)))) =((2π)/( (√3))) another way ∫_(−∞) ^(+∞) (dx/(x^2 +x+1)) =∫_(−∞) ^(+∞) (dx/((x+(1/2))^2 +(3/4))) =_(x+(1/2)=((√3)/2)t) ∫_(−∞) ^(+∞) (1/((3/(4 ))(1+t^2 ))) ((√3)/2)dt =(4/3) ((√3)/2) ∫_(−∞) ^(+∞) (dt/(1+t^2 )) =(2/( (√3))) [arctan(t)]_(−∞) ^(+∞) =(2/( (√3))){(π/2)+(π/2)} =((2π)/( (√3))) . ★ we have g((π/3))=∫_(−∞) ^(+∞) ((sin((π/3)))/((x^2 +x+1)^2 )) dx ⇒ ∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^2 )) =(1/(sin((π/3)))) g((π/3)) =(2/( (√3))) ((π cos((π/3)))/(sin^2 ((π/3)))) =(π/( (√3))) (1/(3/4)) =((4π)/(3(√3))) .
$$\left.\mathrm{4}\right)\:\bigstar{we}\:{have}\:{x}^{\mathrm{2}} +{x}\:+\mathrm{1}\:={x}^{\mathrm{2}} +\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\mathrm{1}\:={x}^{\mathrm{2}} \:+\mathrm{2}{x}\:{cos}\left(\frac{\pi}{\mathrm{3}}\right)+\mathrm{1}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:={f}\left(\frac{\pi}{\mathrm{3}}\right)\:=\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}} \\ $$$${another}\:{way}\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}\:}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}\:=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\left[{arctan}\left({t}\right)\right]_{−\infty} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right\}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:. \\ $$$$\bigstar\:{we}\:{have}\:{g}\left(\frac{\pi}{\mathrm{3}}\right)=\int_{−\infty} ^{+\infty} \:\:\frac{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:{g}\left(\frac{\pi}{\mathrm{3}}\right)\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\frac{\pi\:{cos}\left(\frac{\pi}{\mathrm{3}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *