Question Number 130137 by mathmax by abdo last updated on 22/Jan/21
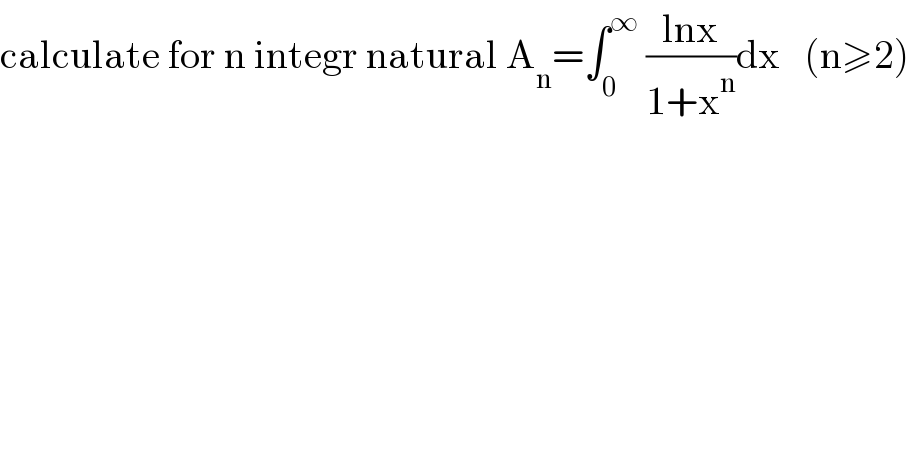
$$\mathrm{calculate}\:\mathrm{for}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{natural}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\:\:\left(\mathrm{n}\geqslant\mathrm{2}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jan/21
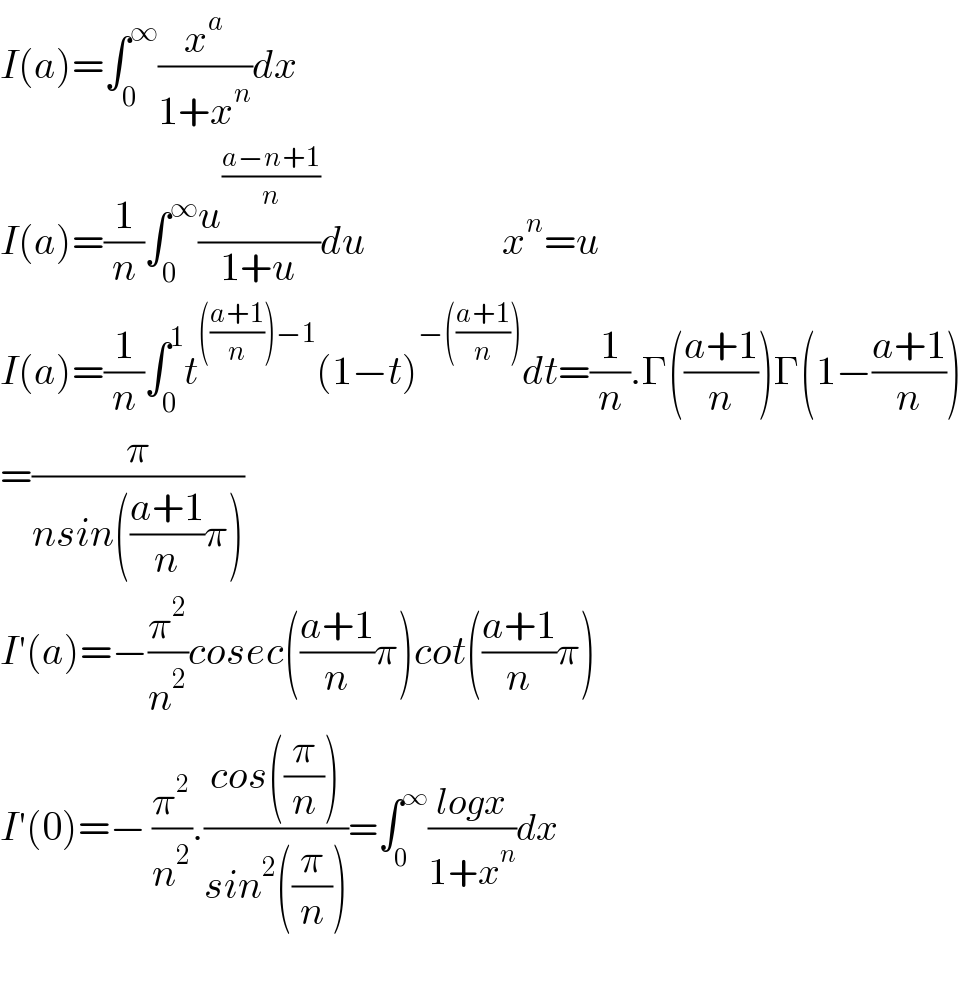
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} }{\mathrm{1}+{x}^{{n}} }{dx} \\ $$$${I}\left({a}\right)=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{{a}−{n}+\mathrm{1}}{{n}}} }{\mathrm{1}+{u}}{du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{{n}} ={u} \\ $$$${I}\left({a}\right)=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\left(\frac{{a}+\mathrm{1}}{{n}}\right)−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{−\left(\frac{{a}+\mathrm{1}}{{n}}\right)} {dt}=\frac{\mathrm{1}}{{n}}.\Gamma\left(\frac{{a}+\mathrm{1}}{{n}}\right)\Gamma\left(\mathrm{1}−\frac{{a}+\mathrm{1}}{{n}}\right) \\ $$$$=\frac{\pi}{{nsin}\left(\frac{{a}+\mathrm{1}}{{n}}\pi\right)} \\ $$$${I}'\left({a}\right)=−\frac{\pi^{\mathrm{2}} }{{n}^{\mathrm{2}} }{cosec}\left(\frac{{a}+\mathrm{1}}{{n}}\pi\right){cot}\left(\frac{{a}+\mathrm{1}}{{n}}\pi\right) \\ $$$${I}'\left(\mathrm{0}\right)=−\:\frac{\pi^{\mathrm{2}} }{{n}^{\mathrm{2}} }.\frac{{cos}\left(\frac{\pi}{{n}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{{n}}\right)}=\int_{\mathrm{0}} ^{\infty} \frac{{logx}}{\mathrm{1}+{x}^{{n}} }{dx} \\ $$$$ \\ $$
Commented by Lordose last updated on 22/Jan/21

$$\mathrm{Nice}\:\mathrm{sir}\: \\ $$
Answered by mathmax by abdo last updated on 23/Jan/21
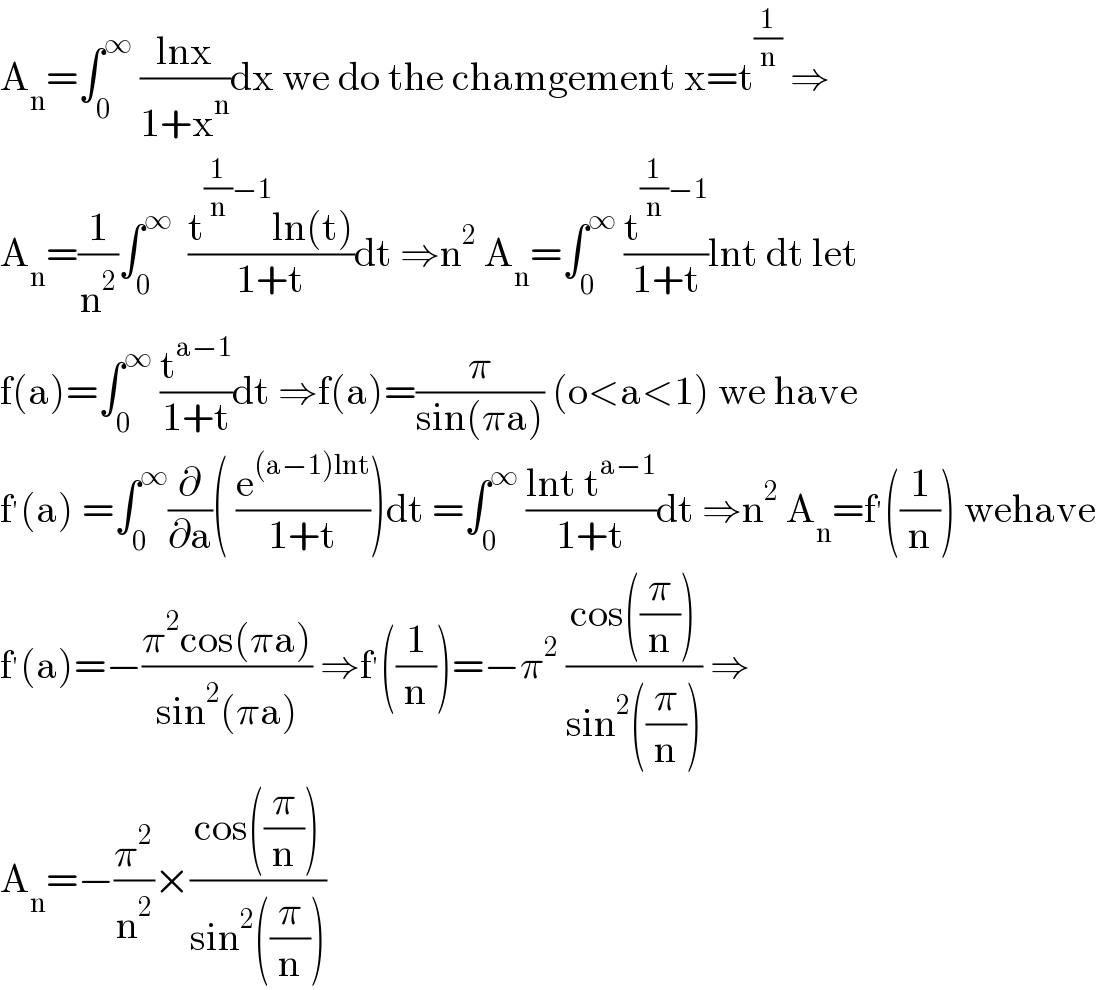
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chamgement}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{n}^{\mathrm{2}} \:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{lnt}\:\mathrm{dt}\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\left(\mathrm{o}<\mathrm{a}<\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial\mathrm{a}}\left(\:\frac{\mathrm{e}^{\left(\mathrm{a}−\mathrm{1}\right)\mathrm{lnt}} }{\mathrm{1}+\mathrm{t}}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}\:\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{n}^{\mathrm{2}} \:\mathrm{A}_{\mathrm{n}} =\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{n}}\right)\:\mathrm{wehave} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\pi^{\mathrm{2}} \mathrm{cos}\left(\pi\mathrm{a}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\pi\mathrm{a}\right)}\:\Rightarrow\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{n}}\right)=−\pi^{\mathrm{2}} \:\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{n}}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{n}}\right)}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =−\frac{\pi^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }×\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{n}}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{n}}\right)} \\ $$
