Question Number 47985 by maxmathsup by imad last updated on 17/Nov/18
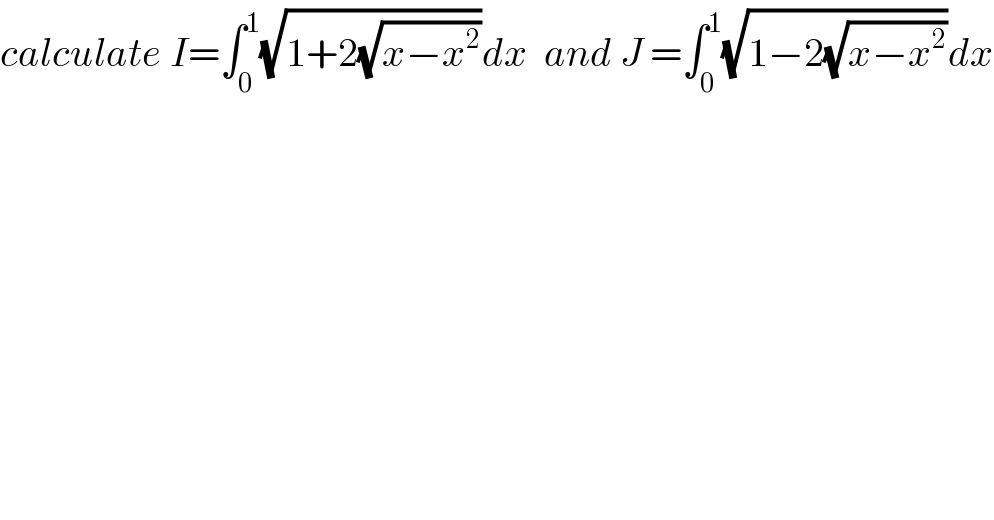
$${calculate}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }}{dx}\:\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }}{dx} \\ $$
Commented by MJS last updated on 18/Nov/18

$${I}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${J}=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{my}\:\mathrm{work}\:\mathrm{later} \\ $$
Commented by maxmathsup by imad last updated on 18/Nov/18
![also we have J =∫_0 ^1 ∣(√x)−(√(1−x))∣dx but x−(1−x)=2x−1 so if 2x−1≥0 ⇒(1/(2 ))≤x≤1 we get ∣(√x)−(√(1−x))∣=(√x)−(√(1−x)) ⇒ ∣(√x)−(√(1−x))∣=(√x)−(√(1−x)) if 2x−1≤0 ⇒0≤x≤(1/2) ⇒∣(√x)−(√(1−x))∣=(√(1−x)) −(√x) ⇒ J =∫_0 ^(1/2) ((√(1−x))−(√x))dx +∫_(1/2) ^1 ((√x)−(√(1−x)))dx ∫_0 ^(1/2) ((√(1−x))−(√x))dx=[−(2/3)(1−x)^(3/2) −(2/3) x^(3/2) ]_0 ^(1/2) =(2/3) −(2/3)((1/2))^(3/2) −(2/3)((1/2))^(3/2) =(2/3) −(4/3) (1/2^(3/2) ) =(2/3) −(2^(2−(3/2)) /3) =(2/3) −((√2)/3) ∫_(1/2) ^1 ((√x)−(√(1−x)))dx =[(2/3)x^(3/2) +(2/3)(1−x)^(3/2) ]_(1/2) ^1 =(2/3) −(2/3)((1/2))^(3/2) −(2/3)((1/2))^(3/2) =(2/3) −(4/3)((1/2))^(3/2) =(2/3) −((√2)/3) ⇒ J=2((2/3) −((√2)/3))=(4/3) −((2(√2))/3) .](https://www.tinkutara.com/question/Q48039.png)
$${also}\:{we}\:{have}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mid\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\mid{dx}\:\:\:{but}\:{x}−\left(\mathrm{1}−{x}\right)=\mathrm{2}{x}−\mathrm{1}\:{so} \\ $$$${if}\:\:\mathrm{2}{x}−\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\:}\leqslant{x}\leqslant\mathrm{1}\:{we}\:{get}\:\mid\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\mid=\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\:\Rightarrow \\ $$$$\mid\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\mid=\sqrt{{x}}−\sqrt{\mathrm{1}−{x}} \\ $$$${if}\:\mathrm{2}{x}−\mathrm{1}\leqslant\mathrm{0}\:\Rightarrow\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mid\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\mid=\sqrt{\mathrm{1}−{x}}\:−\sqrt{{x}}\:\Rightarrow \\ $$$${J}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\sqrt{\mathrm{1}−{x}}−\sqrt{{x}}\right){dx}\:+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \left(\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\sqrt{\mathrm{1}−{x}}−\sqrt{{x}}\right){dx}=\left[−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\frac{\mathrm{2}}{\mathrm{3}}\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{2}^{\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}\:=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \left(\sqrt{{x}}−\sqrt{\mathrm{1}−{x}}\right){dx}\:=\left[\frac{\mathrm{2}}{\mathrm{3}}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:=\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\:\Rightarrow\:{J}=\mathrm{2}\left(\frac{\mathrm{2}}{\mathrm{3}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\right)=\frac{\mathrm{4}}{\mathrm{3}}\:−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:. \\ $$
Commented by maxmathsup by imad last updated on 18/Nov/18
![we have first 1+2(√(x−x^2 ))=1+2(√x)(√(1−x))=x +1−x+2(√x)(√(1−x)) =((√x)+(√(1−x)))^2 ⇒(√(1+2(√(x−x^2 ))))=∣(√x)+(√(1−x))∣ but x∈[0,1] ⇒∣(√(x+(√(1−x))))∣= (√x)+(√(1−x)) ⇒I =∫_0 ^1 ((√x)+(√(1−x)))dx =∫_0 ^1 (√x)dx +∫_0 ^1 (√(1−x))dx =[(2/3)x^(3/2) ]_0 ^1 +[−(2/3)(1−x)^(3/2) ]_0 ^1 =(2/3) +(2/3) =(4/3)](https://www.tinkutara.com/question/Q48015.png)
$${we}\:{have}\:{first}\:\:\mathrm{1}+\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }=\mathrm{1}+\mathrm{2}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}={x}\:+\mathrm{1}−{x}+\mathrm{2}\sqrt{{x}}\sqrt{\mathrm{1}−{x}} \\ $$$$=\left(\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\right)^{\mathrm{2}} \:\Rightarrow\sqrt{\mathrm{1}+\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }}=\mid\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\mid\:{but}\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:\Rightarrow\mid\sqrt{{x}+\sqrt{\mathrm{1}−{x}}}\mid= \\ $$$$\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}}{dx} \\ $$$$=\left[\frac{\mathrm{2}}{\mathrm{3}}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:\:+\left[−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{3}}\:=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Nov/18

$$\mathrm{1}+\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} }\: \\ $$$$\mathrm{1}+\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}\: \\ $$$${x}+\mathrm{1}−{x}+\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}\: \\ $$$$\left\{\sqrt{{x}}\:+\sqrt{\mathrm{1}−{x}}\:\right\}^{\mathrm{2}} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}\:+\sqrt{\mathrm{1}−{x}}\:{dx} \\ $$$${now}\: \\ $$$$=\mid\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\mathrm{3}}{\mathrm{2}}}\mid_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{2}}{\mathrm{3}}\mid\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${J}= \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} \sqrt{\mathrm{1}−\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}}\:{dx}+\int_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} \sqrt{\mathrm{1}−{x}}\:−\sqrt{{x}}\:{dx}+\int_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} \sqrt{{x}}\:−\sqrt{\mathrm{1}−{x}}\:{dx} \\ $$$${from}\mathrm{0}.\mathrm{5}\:>{x}>\mathrm{0}\:\:\:{value}\:{of}\:\sqrt{\mathrm{1}−{x}}\:>{value}\:{of}\:\sqrt{{x}}\: \\ $$$${and}\:{from}\:\mathrm{1}>{x}>\mathrm{0}.\mathrm{5}\:\:{valud}\:{of}\:\sqrt{{x}}\:>\sqrt{\mathrm{1}−{x}}\: \\ $$$${so} \\ $$$$ \\ $$$$=\mid\left\{−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{3}}\left({x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}\mid_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} +\mid\left\{\frac{\mathrm{2}}{\mathrm{3}}\left({x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}\mid_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} \\ $$$$=\left(−\frac{\mathrm{2}}{\mathrm{3}}\right)\left\{\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{0}\right\}+\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{1}+\mathrm{0}−\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\} \\ $$$$=\left(\frac{−\mathrm{4}}{\mathrm{3}}\right)\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}−\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{3}}×\left(\mathrm{0}.\mathrm{5}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:} \\ $$
