Menu Close

calculate-I-0-1-e-2t-ln-1-e-t-dt-

Tinku Tara 0 Comments
Pin




Question Number 35684 by prof Abdo imad last updated on 22/May/18
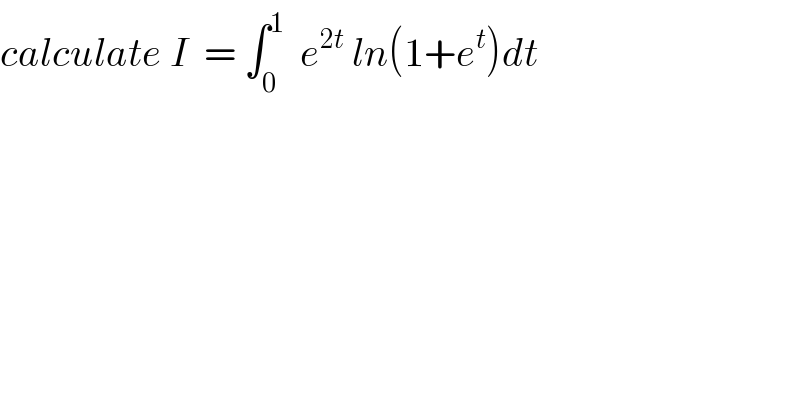
calculate I = ∫_0 ^1 e^(2t) ln(1+e^t )dt
$${calculate}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{\mathrm{2}{t}} \:{ln}\left(\mathrm{1}+{e}^{{t}} \right){dt} \\ $$
Commented by prof Abdo imad last updated on 22/May/18
let put I = ∫_0 ^1 e^(2t) ln(1+e^t )dt .changement e^t =x give I = ∫_1 ^e x^2 ln(1+x)(dx/x) = ∫_1 ^e xln(1+x)dx .by parts we get I = [ (x^2 /2)ln(1+x)]_1 ^e −∫_1 ^e (x^2 /2) (dx/(1+x)) =(e^2 /2)ln(1+e) −(1/2)ln(2) −(1/2) ∫_1 ^e (x^2 /(1+x))dx ∫_1 ^e (x^2 /(x+1))dx = ∫_1 ^e ((x^2 −1 +1)/(x+1))dx = ∫_1 ^e (x−1)dx + ∫_1 ^e (dx/(x+1)) =[ (x^2 /2) −x]_1 ^e + [ln(x+1)]_1 ^e =(e^2 /2) −e −(1/2) +1 +ln(1+e) −ln(2) ⇒ I = (e^2 /2)ln(1+e) −(1/2)ln(2)−(1/4)e^2 +(1/2)e −(1/4) +ln(1+e) −ln(2) ={ 1+(e^2 /2)}ln(1+e) −(3/2)ln(2) −(e^2 /4) +(e/2)−(1/4).
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{\mathrm{2}{t}} \:{ln}\left(\mathrm{1}+{e}^{{t}} \right){dt}\:.{changement} \\ $$$${e}^{{t}} \:={x}\:{give}\:{I}\:=\:\int_{\mathrm{1}} ^{{e}} \:\:\:{x}^{\mathrm{2}} {ln}\left(\mathrm{1}+{x}\right)\frac{{dx}}{{x}} \\ $$$$=\:\int_{\mathrm{1}} ^{{e}} \:{xln}\left(\mathrm{1}+{x}\right){dx}\:\:\:.{by}\:{parts}\:{we}\:{get} \\ $$$${I}\:=\:\left[\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{1}} ^{{e}} \:\:−\int_{\mathrm{1}} ^{{e}} \:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$=\frac{{e}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\mathrm{1}+{e}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{{e}} \:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}{dx} \\ $$$$\int_{\mathrm{1}} ^{{e}} \:\:\frac{{x}^{\mathrm{2}} }{{x}+\mathrm{1}}{dx}\:=\:\int_{\mathrm{1}} ^{{e}} \:\:\frac{{x}^{\mathrm{2}} \:−\mathrm{1}\:+\mathrm{1}}{{x}+\mathrm{1}}{dx} \\ $$$$=\:\int_{\mathrm{1}} ^{{e}} \:\:\left({x}−\mathrm{1}\right){dx}\:\:+\:\int_{\mathrm{1}} ^{{e}} \:\:\:\frac{{dx}}{{x}+\mathrm{1}} \\ $$$$=\left[\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−{x}\right]_{\mathrm{1}} ^{{e}} \:\:+\:\left[{ln}\left({x}+\mathrm{1}\right)\right]_{\mathrm{1}} ^{{e}} \\ $$$$=\frac{{e}^{\mathrm{2}} }{\mathrm{2}}\:−{e}\:−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{1}\:+{ln}\left(\mathrm{1}+{e}\right)\:−{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${I}\:\:=\:\frac{{e}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\mathrm{1}+{e}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}{e}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$+{ln}\left(\mathrm{1}+{e}\right)\:−{ln}\left(\mathrm{2}\right) \\ $$$$=\left\{\:\mathrm{1}+\frac{{e}^{\mathrm{2}} }{\mathrm{2}}\right\}{ln}\left(\mathrm{1}+{e}\right)\:−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:−\frac{{e}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{{e}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18
=∫_0 ^1 e^(2t) (e^t −(e^(2t) /2)+(e^(3t) /3)−((e^(4t) )/4)+...)dt =∫_0 ^1 e^(3t) −(e^(4t) /2)+(e^(5t) /3)−(e^(6t_ ) /4)+... dt =∣(e^(3t) /3)−(e^(4t) /(2×4))+(e^(5t) /(3×5))−(e^(6t) /(4×6))+....∣_0 ^1 =((e^3 /3)−(e^4 /(2×4))+(e^5 /(3×5))−(e^6 /(4×6))...)−( (1/3)−(1/(2×4))+(1/(3×5)) −(1/(4×6))+....) let s_1 =sum total of first s_(2 ) =sum total of second T_n =(−1)^(n−1) {(1/(n×(n+2)))} general term for s_2 T_n =(1/2)×(−1)^(n−1) ×{(1/n)−(1/(n+2))} T_1 =(1/2)×1×{(1/1)−(1/3)} T_2 =(1/2)×1×{(1/4)−(1/2)} T_3 =(1/2)×1×{(1/3)−(1/5)} .......... ........... adding we get (1/2)×1×{1−(1/2)} other terms cancelled so s_2 =(1/2)×(1/2)=(1/4) contd to find s_1 T_n =(−1)^(n−1) ×{(e^(n+2) /(n×(n+2)))} =(−1)^(n−1) ×e^(n+2) ×(1/2)×((1/n)−(1/(n+2))) contd
$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{t}} \left({e}^{{t}} −\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}+\frac{{e}^{\mathrm{3}{t}} }{\mathrm{3}}−\frac{{e}^{\mathrm{4}{t}} \:}{\mathrm{4}}+…\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{3}{t}} −\frac{{e}^{\mathrm{4}{t}} }{\mathrm{2}}+\frac{{e}^{\mathrm{5}{t}} }{\mathrm{3}}−\frac{{e}^{\mathrm{6}{t}_{} } }{\mathrm{4}}+…\:\:\:{dt} \\ $$$$=\mid\frac{{e}^{\mathrm{3}{t}} }{\mathrm{3}}−\frac{{e}^{\mathrm{4}{t}} }{\mathrm{2}×\mathrm{4}}+\frac{{e}^{\mathrm{5}{t}} }{\mathrm{3}×\mathrm{5}}−\frac{{e}^{\mathrm{6}{t}} }{\mathrm{4}×\mathrm{6}}+….\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left(\frac{{e}^{\mathrm{3}} }{\mathrm{3}}−\frac{{e}^{\mathrm{4}} }{\mathrm{2}×\mathrm{4}}+\frac{{e}^{\mathrm{5}} }{\mathrm{3}×\mathrm{5}}−\frac{{e}^{\mathrm{6}} }{\mathrm{4}×\mathrm{6}}…\right)−\left(\:\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{5}}\right. \\ $$$$\left.−\frac{\mathrm{1}}{\mathrm{4}×\mathrm{6}}+….\right) \\ $$$${let}\:{s}_{\mathrm{1}} ={sum}\:{total}\:{of}\:{first}\: \\ $$$$\:\:\:{s}_{\mathrm{2}\:} ={sum}\:{total}\:{of}\:{second} \\ $$$${T}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left\{\frac{\mathrm{1}}{{n}×\left({n}+\mathrm{2}\right)}\right\}\:\:{general}\:{term}\:{for}\:{s}_{\mathrm{2}} \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}×\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×\left\{\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right\} \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\left\{\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\right\} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\left\{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\left\{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right\} \\ $$$$………. \\ $$$$……….. \\ $$$${adding}\:{we}\:{get}\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}×\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right\}\:\:{other}\:{terms} \\ $$$${cancelled} \\ $$$${so}\:\:{s}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${contd}\:{to}\:{find}\:{s}_{\mathrm{1}} \\ $$$${T}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×\left\{\frac{{e}^{{n}+\mathrm{2}} }{{n}×\left({n}+\mathrm{2}\right)}\right\} \\ $$$$=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×{e}^{{n}+\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$${contd} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *