Menu Close

calculate-I-0-1-ln-1-t-2-4-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 38463 by maxmathsup by imad last updated on 25/Jun/18
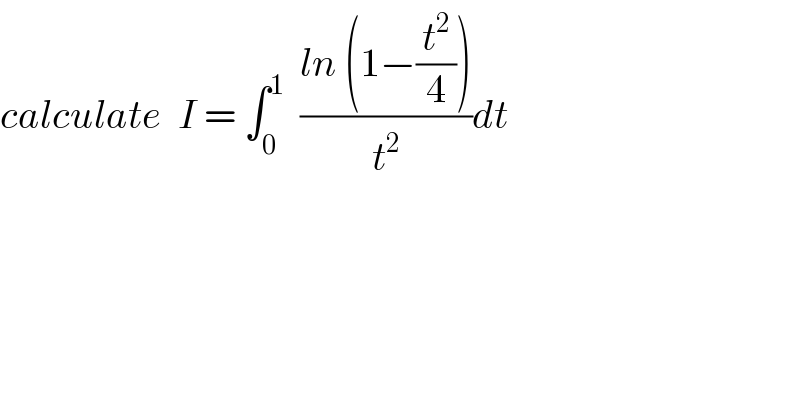
calculate I = ∫_0 ^1 ((ln (1−(t^2 /4)))/t^2 )dt
$${calculate}\:\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\:\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\right)}{{t}^{\mathrm{2}} }{dt}\: \\ $$
Commented by abdo mathsup 649 cc last updated on 05/Jul/18
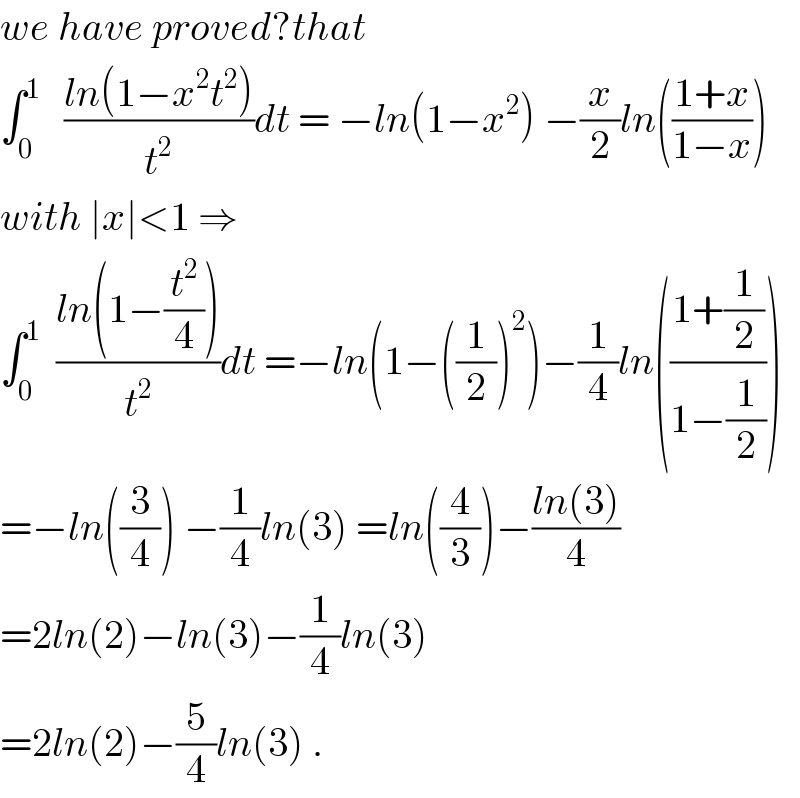
we have proved?that ∫_0 ^1 ((ln(1−x^2 t^2 ))/t^2 )dt = −ln(1−x^2 ) −(x/2)ln(((1+x)/(1−x))) with ∣x∣<1 ⇒ ∫_0 ^1 ((ln(1−(t^2 /4)))/t^2 )dt =−ln(1−((1/2))^2 )−(1/4)ln(((1+(1/2))/(1−(1/2)))) =−ln((3/4)) −(1/4)ln(3) =ln((4/3))−((ln(3))/4) =2ln(2)−ln(3)−(1/4)ln(3) =2ln(2)−(5/4)ln(3) .
$${we}\:{have}\:{proved}?{that}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }{dt}\:=\:−{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:−\frac{{x}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$${with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\right)}{{t}^{\mathrm{2}} }{dt}\:=−{ln}\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right) \\ $$$$=−{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)\:={ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)−\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{4}}\: \\ $$$$=\mathrm{2}{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{3}\right) \\ $$$$=\mathrm{2}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{5}}{\mathrm{4}}{ln}\left(\mathrm{3}\right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *