Menu Close

calculate-I-0-2pi-cos-2x-cosx-sinx-dx-and-J-0-2pi-sin-2x-cosx-sinx-dx-

Tinku Tara 0 Comments
Pin




Question Number 42500 by maxmathsup by imad last updated on 26/Aug/18
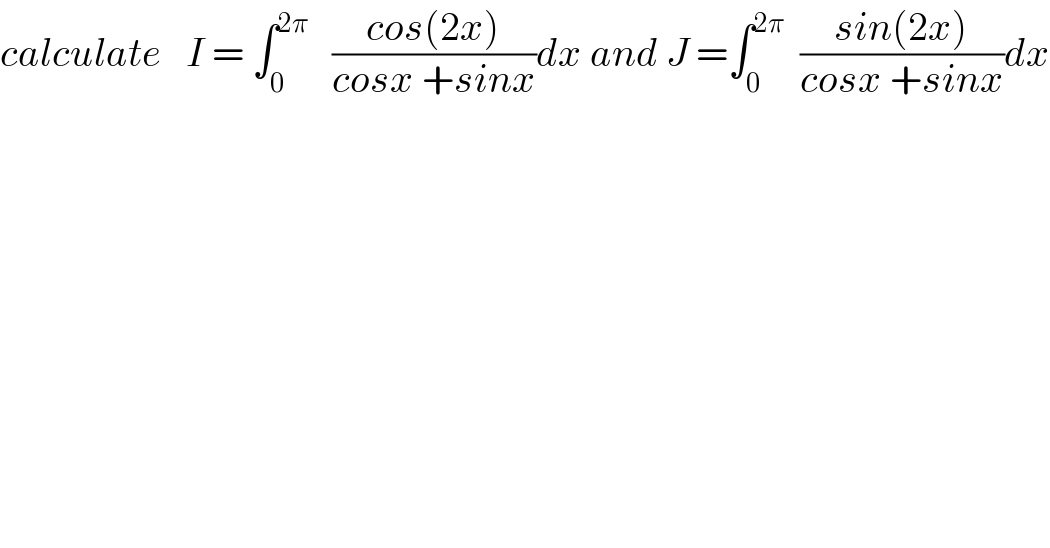
calculate I = ∫_0 ^(2π) ((cos(2x))/(cosx +sinx))dx and J =∫_0 ^(2π) ((sin(2x))/(cosx +sinx))dx
$${calculate}\:\:\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{{cosx}\:+{sinx}}{dx}\:{and}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{{cosx}\:+{sinx}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18
we have I = Re( ∫_0 ^(2π) (e^(i2x) /(cosx +sinx))dx) changement e^(ix) =z give ∫_0 ^(2π) (e^(i2x) /(cosx +sonx))dx = ∫_(∣z∣=1) (z^2 /(((z+z^(−1) )/2) +((z−z^(−1) )/(2i)))) (dz/(iz)) = ∫_(∣z∣=1) ((2z^2 )/(iz{ z+z^(−1) −i(z−z^(−1) )}))dz =∫_(∣z∣=1) ((2z^2 )/(iz^2 +i +z^2 −1))dz =∫_(∣z∣=1) ((2z^2 )/((1+i)z^2 +i−1))dz let ϕ(z) =((2z^2 )/((1+i)z^2 +i−1)) poles of ϕ? ϕ(z) =((2z^2 )/((1+i)(z^2 −((1−i)/(1+i))))) =((2z^2 )/((1+i)(z^2 −(((1−i)^2 )/2)))) =((2z^2 )/((1+i)(z^2 +i))) =((2z^2 )/((1+i)(z−(√(−i)))(z+(√(−i))))) =((2z^2 )/((1+i)(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) so the poles of ϕ are +^− e^(−((iπ)/4)) ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ{ Res(ϕ,e^(−((iπ)/4)) ) +Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^(−((iπ)/4)) ) =lim_(z→e^(−((iπ)/4)) ) (z−e^(−((iπ)/4)) )ϕ(z) = ((2 (−i))/((1+i)2e^(−((iπ)/4)) )) =((−i)/(1+i)) e^((iπ)/4) =((−i(1−i))/2) e^((iπ)/4) =((−1−i)/2) e^((iπ)/4) Res(ϕ,−e^(−((iπ)/4)) ) =lim_(z→−e^(−((iπ)/4)) ) (z+e^((iπ)/4) )ϕ(z) =((2(−i))/((1+i)(−2 e^(−((iπ)/4)) ))) =(i/(1+i)) e^((iπ)/4) =((i(1−i))/2) e^((iπ)/4) =((1+i)/2) e^((iπ)/4) ⇒ ∫_(∣z∣ =1) ϕ(z)dz =2iπ{((−1−i)/2) e^((iπ)/4) +((1+i)/2) e^((iπ)/4) } =0 ⇒ I =0 and J =0 .
$${we}\:{have}\:{I}\:=\:{Re}\left(\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{e}^{{i}\mathrm{2}{x}} }{{cosx}\:+{sinx}}{dx}\right)\:\:{changement}\:\:{e}^{{ix}} \:={z}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{e}^{{i}\mathrm{2}{x}} }{{cosx}\:+{sonx}}{dx}\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\frac{{z}^{\mathrm{2}} }{\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\:+\frac{{z}−{z}^{−\mathrm{1}} }{\mathrm{2}{i}}}\:\frac{{dz}}{{iz}} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{2}{z}^{\mathrm{2}} }{{iz}\left\{\:{z}+{z}^{−\mathrm{1}} \:−{i}\left({z}−{z}^{−\mathrm{1}} \right)\right\}}{dz}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{z}^{\mathrm{2}} }{{iz}^{\mathrm{2}} \:+{i}\:+{z}^{\mathrm{2}} −\mathrm{1}}{dz} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right){z}^{\mathrm{2}} \:+{i}−\mathrm{1}}{dz}\:\:{let}\:\varphi\left({z}\right)\:=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right){z}^{\mathrm{2}} \:+{i}−\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right)\left({z}^{\mathrm{2}} \:−\frac{\mathrm{1}−{i}}{\mathrm{1}+{i}}\right)}\:=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right)\left({z}^{\mathrm{2}} \:−\frac{\left(\mathrm{1}−{i}\right)^{\mathrm{2}} }{\mathrm{2}}\right)}\:=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)} \\ $$$$=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right)\left({z}−\sqrt{−{i}}\right)\left({z}+\sqrt{−{i}}\right)}\:=\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{i}\right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are} \\ $$$$\overset{−} {+}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\:\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\varphi\left({z}\right)\:=\:\frac{\mathrm{2}\:\left(−{i}\right)}{\left(\mathrm{1}+{i}\right)\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:=\frac{−{i}}{\mathrm{1}+{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$$=\frac{−{i}\left(\mathrm{1}−{i}\right)}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:=\frac{−\mathrm{1}−{i}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\varphi\left({z}\right)\:=\frac{\mathrm{2}\left(−{i}\right)}{\left(\mathrm{1}+{i}\right)\left(−\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\frac{{i}}{\mathrm{1}+{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:=\frac{{i}\left(\mathrm{1}−{i}\right)}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:=\frac{\mathrm{1}+{i}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\int_{\mid{z}\mid\:=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{−\mathrm{1}−{i}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:+\frac{\mathrm{1}+{i}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right\}\:=\mathrm{0}\:\Rightarrow\:{I}\:=\mathrm{0}\:{and}\:{J}\:=\mathrm{0}\:. \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18
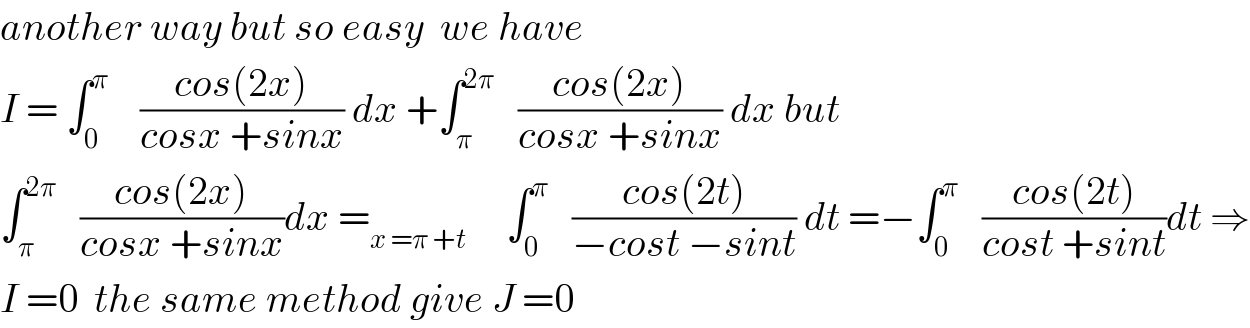
another way but so easy we have I = ∫_0 ^π ((cos(2x))/(cosx +sinx)) dx +∫_π ^(2π) ((cos(2x))/(cosx +sinx)) dx but ∫_π ^(2π) ((cos(2x))/(cosx +sinx))dx =_(x =π +t) ∫_0 ^π ((cos(2t))/(−cost −sint)) dt =−∫_0 ^π ((cos(2t))/(cost +sint))dt ⇒ I =0 the same method give J =0
$${another}\:{way}\:{but}\:{so}\:{easy}\:\:{we}\:{have}\: \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{{cosx}\:+{sinx}}\:{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{{cosx}\:+{sinx}}\:{dx}\:{but} \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{{cosx}\:+{sinx}}{dx}\:=_{{x}\:=\pi\:+{t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{−{cost}\:−{sint}}\:{dt}\:=−\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{{cost}\:+{sint}}{dt}\:\Rightarrow \\ $$$${I}\:=\mathrm{0}\:\:{the}\:{same}\:{method}\:{give}\:{J}\:=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *