Question Number 44002 by maxmathsup by imad last updated on 19/Sep/18
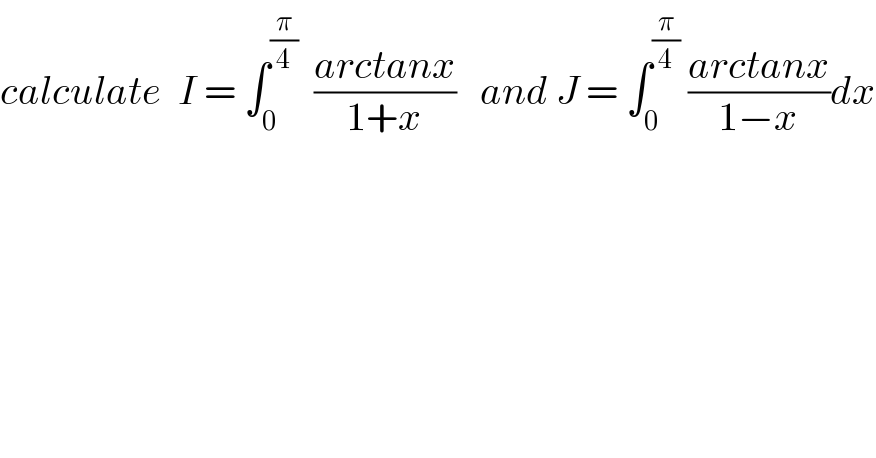
$${calculate}\:\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{arctanx}}{\mathrm{1}+{x}}\:\:\:{and}\:{J}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{arctanx}}{\mathrm{1}−{x}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 24/Sep/18
![let f(α) =∫_0 ^(π/4) ((arctan(αx))/(1+x))dx ⇒I =f(1) we have f^′ (α) = ∫_0 ^(π/4) ((x dx)/((1+x)(1+α^2 x^2 ))) =_(αx =t) ∫_0 ^((απ)/4) ((tdt)/(α(1+(t/α))(1+t^2 ))) = ∫_0 ^((απ)/4) ((tdt)/((t+α)(t^2 +1))) let decompose F(t) = (t/((t+α)(t^2 +1))) F(t) = (a/(t+α)) +((bt +c)/(t^2 +1)) we have a=lim_(t→−α) (t+α)F(t)=((−α)/(1+α^2 )) lim_(t→+∞) t F(t) =0 =a+b ⇒b =(α/(1+α^2 )) ⇒F(t)=−(α/((1+α^2 )(t+α))) +(((α/(1+α^2 ))t +c)/(1+t^2 )) F(0)=0 = −(α/((1+α^2 )α)) +c ⇒c =(1/(1+α^2 )) ⇒ F(t) = −(α/((1+α^2 )(t+α))) +(1/(1+α^2 )) ((αt +1)/(t^2 +1)) ⇒ f^′ (α) =((−α)/(1+α^2 )) ∫_0 ^((απ)/4) (dt/(t+α)) +(1/(1+α^2 )) ∫_0 ^((απ)/4) ((αt +1)/(t^(2 ) +1))dt but ∫_0 ^((απ)/4) (dt/(t+α)) =[ln∣t+α∣]_0 ^((απ)/4) =ln∣((απ)/4)+α∣−ln∣α∣ =ln∣1+(π/4)∣ ∫_0 ^((απ)/4) ((αt +1)/(t^2 +1)) dt =(α/2)[ln(t^2 +1)]_0 ^((απ)/4) +arctan(((απ)/4)) =(α/2)ln(1+((α^2 π^2 )/(16))) +arctan(((απ)/4)) ⇒ f^′ (α) =((−α)/(1+α^2 ))ln(1+(π/4)) + (α/(2(1+α^2 )))ln(1+((α^2 π^2 )/(16))) +(1/(1+α^2 ))arctan(((απ)/4)) ⇒ f(α) =−ln(1+(π/4)) ∫_0 ^α (x/(1+x^2 ))dx +(1/2) ∫_0 ^α (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^α (1/(1+x^2 ))arctan(((πx)/4))dx +c ( c=f(0)=0) ⇒ f(1) =−ln(1+(π/4)) ∫_0 ^1 (x/(1+x^2 ))dx +(1/2) ∫_0 ^1 (x/(1+x^2 ))ln(1+((x^2 π^2 )/(16)))dx +∫_0 ^1 ((arctan(((πx)/4)))/(1+x^2 ))dx ....be continued...](https://www.tinkutara.com/question/Q44246.png)
$${let}\:{f}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{arctan}\left(\alpha{x}\right)}{\mathrm{1}+{x}}{dx}\:\Rightarrow{I}\:={f}\left(\mathrm{1}\right)\:{we}\:{have} \\ $$$${f}^{'} \left(\alpha\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{x}\:{dx}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\alpha^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:=_{\alpha{x}\:={t}} \:\:\:\:\:\:\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{tdt}}{\alpha\left(\mathrm{1}+\frac{{t}}{\alpha}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\:\frac{{tdt}}{\left({t}+\alpha\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{let}\:{decompose}\:{F}\left({t}\right)\:=\:\frac{{t}}{\left({t}+\alpha\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)\:=\:\frac{{a}}{{t}+\alpha}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:{we}\:{have}\:{a}={lim}_{{t}\rightarrow−\alpha} \left({t}+\alpha\right){F}\left({t}\right)=\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\Rightarrow{F}\left({t}\right)=−\frac{\alpha}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left({t}+\alpha\right)}\:+\frac{\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{t}\:+{c}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}\:=\:−\frac{\alpha}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\alpha}\:+{c}\:\Rightarrow{c}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:−\frac{\alpha}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left({t}+\alpha\right)}\:+\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\:\frac{\alpha{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${f}^{'} \left(\alpha\right)\:=\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{{t}+\alpha}\:\:+\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\frac{\alpha{t}\:+\mathrm{1}}{{t}^{\mathrm{2}\:} +\mathrm{1}}{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\frac{{dt}}{{t}+\alpha}\:=\left[{ln}\mid{t}+\alpha\mid\right]_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:={ln}\mid\frac{\alpha\pi}{\mathrm{4}}+\alpha\mid−{ln}\mid\alpha\mid\:={ln}\mid\mathrm{1}+\frac{\pi}{\mathrm{4}}\mid\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:\:\frac{\alpha{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\frac{\alpha}{\mathrm{2}}\left[{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\frac{\alpha\pi}{\mathrm{4}}} \:\:+{arctan}\left(\frac{\alpha\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\alpha}{\mathrm{2}}{ln}\left(\mathrm{1}+\frac{\alpha^{\mathrm{2}} \pi^{\mathrm{2}} }{\mathrm{16}}\right)\:+{arctan}\left(\frac{\alpha\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${f}^{'} \left(\alpha\right)\:=\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{ln}\left(\mathrm{1}+\frac{\pi}{\mathrm{4}}\right)\:+\:\frac{\alpha}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\left(\mathrm{1}+\frac{\alpha^{\mathrm{2}} \pi^{\mathrm{2}} }{\mathrm{16}}\right)\:+\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }{arctan}\left(\frac{\alpha\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$${f}\left(\alpha\right)\:=−{ln}\left(\mathrm{1}+\frac{\pi}{\mathrm{4}}\right)\:\int_{\mathrm{0}} ^{\alpha} \:\:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\alpha} \:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{ln}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} \pi^{\mathrm{2}} }{\mathrm{16}}\right){dx}\:+\int_{\mathrm{0}} ^{\alpha} \:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{arctan}\left(\frac{\pi{x}}{\mathrm{4}}\right){dx} \\ $$$$+{c}\:\left(\:{c}={f}\left(\mathrm{0}\right)=\mathrm{0}\right)\:\Rightarrow \\ $$$${f}\left(\mathrm{1}\right)\:=−{ln}\left(\mathrm{1}+\frac{\pi}{\mathrm{4}}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{ln}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} \pi^{\mathrm{2}} }{\mathrm{16}}\right){dx} \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left(\frac{\pi{x}}{\mathrm{4}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:….{be}\:{continued}… \\ $$$$ \\ $$
