Question Number 41703 by abdo.msup.com last updated on 11/Aug/18
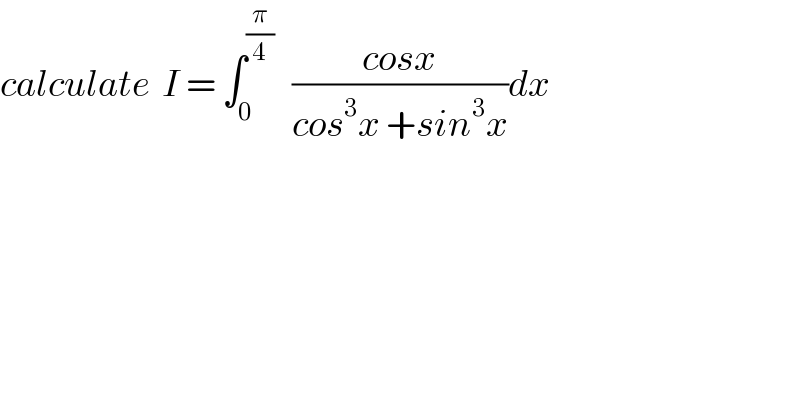
$${calculate}\:\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{cosx}}{{cos}^{\mathrm{3}} {x}\:+{sin}^{\mathrm{3}} {x}}{dx} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
![I = ∫_0 ^(π/4) (((cosx)/(cos^3 x))/((cos^3 x +sin^3 x)/(cos^3 x))) dx =∫_0 ^(π/4) (1/(cos^2 x(1+tan^3 x)))dx =∫_0 ^(π/4) ((1+tan^2 x)/(1+tan^3 x)) dx =_(tanx=t) ∫_0 ^1 ((1+t^2 )/(1+t^3 )) (dt/(1+t^2 )) = ∫_0 ^1 (dt/(1+t^3 )) let decompose F(t)= (1/(t^3 +1)) =(1/((t+1)(t^2 −t +1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t) =(1/3) lim_(t→+∞) tF(t)=0=a +b ⇒b=−(1/3) ⇒ F(t) = (1/(3(t+1))) +((−(1/3)t +c)/(t^2 −t +1)) F(0) =1 =(1/3) +c ⇒c=(2/3) ⇒ F(t) = (1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t +1)) ⇒ ∫_0 ^1 F(t)dt =(1/3)[ln∣t+1∣]_0 ^1 −(1/3) ∫_0 ^1 ((t−2)/(t^2 −t +1))dt =((ln(2))/3) −(1/6) ∫_0 ^1 ((2t−1−3)/(t^2 −t +1)) dt =((ln(2))/3) −[(1/6)ln∣t^2 −t+1∣ ]_0 ^1 +(1/2) ∫_0 ^1 (dt/(t^2 −t +1)) =((ln(2))/3) +(1/2) ∫_0 ^1 (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) ((ln(2))/3) +(1/2) (4/3) ∫_(−(1/( (√3)))) ^(1/( (√3))) (1/(1+u^2 )) ((√3)/2) du =((ln(2))/3) + ((√3)/3) [ arctanu]_(−(1/( (√3)))) ^(1/( (√3))) =((ln(2))/3) + (1/( (√3))){ 2 arctan((1/( (√3))))} =((ln(2))/3) +(2/( (√3))) (π/6) ⇒ I = ((ln(2))/3) +(π/(3(√3))) .](https://www.tinkutara.com/question/Q41758.png)
$${I}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\frac{{cosx}}{{cos}^{\mathrm{3}} {x}}}{\frac{{cos}^{\mathrm{3}} {x}\:+{sin}^{\mathrm{3}} {x}}{{cos}^{\mathrm{3}} {x}}}\:{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}\left(\mathrm{1}+{tan}^{\mathrm{3}} {x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{tan}^{\mathrm{3}} {x}}\:{dx}\:=_{{tanx}={t}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{3}} }\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{3}} }\:\:{let}\:{decompose}\: \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}\:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)=\mathrm{0}={a}\:+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}\left({t}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{3}}{t}\:+{c}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{t}−\mathrm{2}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\left[{ln}\mid{t}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}−\mathrm{2}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{t}−\mathrm{1}−\mathrm{3}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:{dt} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:−\left[\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{t}^{\mathrm{2}} −{t}+\mathrm{1}\mid\:\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{t}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{4}}{\mathrm{3}}\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{du} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:\:+\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\left[\:{arctanu}\right]_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left\{\:\mathrm{2}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\frac{\pi}{\mathrm{6}}\:\Rightarrow\:{I}\:=\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:. \\ $$
