Menu Close

Calculate-i-cos-arctan-x-ii-cos-arcsin-x-iii-tan-arcsin-x-

Tinku Tara 0 Comments
Pin




Question Number 93239 by Ar Brandon last updated on 11/May/20
Calculate; i) cos(arctan x) ii) cos(arcsin x) iii) tan(arcsin x)
$$\mathrm{Calculate}; \\ $$$$\left.{i}\right)\:\mathrm{cos}\left(\mathrm{arctan}\:{x}\right) \\ $$$$\left.{ii}\right)\:\mathrm{cos}\left(\mathrm{arcsin}\:{x}\right) \\ $$$$\left.{iii}\right)\:\mathrm{tan}\left(\mathrm{arcsin}\:{x}\right) \\ $$
Commented by mathmax by abdo last updated on 12/May/20
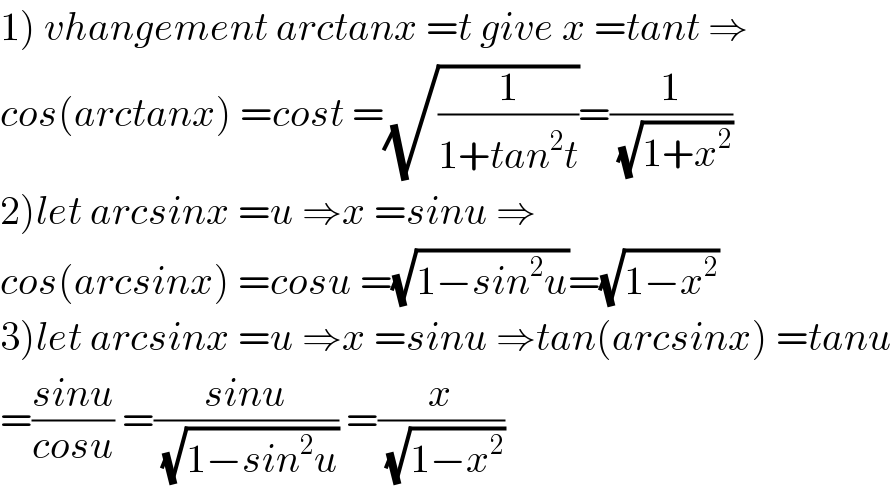
1) vhangement arctanx =t give x =tant ⇒ cos(arctanx) =cost =(√(1/(1+tan^2 t)))=(1/( (√(1+x^2 )))) 2)let arcsinx =u ⇒x =sinu ⇒ cos(arcsinx) =cosu =(√(1−sin^2 u))=(√(1−x^2 )) 3)let arcsinx =u ⇒x =sinu ⇒tan(arcsinx) =tanu =((sinu)/(cosu)) =((sinu)/( (√(1−sin^2 u)))) =(x/( (√(1−x^2 ))))
$$\left.\mathrm{1}\right)\:{vhangement}\:{arctanx}\:={t}\:{give}\:{x}\:={tant}\:\Rightarrow \\ $$$${cos}\left({arctanx}\right)\:={cost}\:=\sqrt{\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{2}\right){let}\:{arcsinx}\:={u}\:\Rightarrow{x}\:={sinu}\:\Rightarrow \\ $$$${cos}\left({arcsinx}\right)\:={cosu}\:=\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {u}}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){let}\:{arcsinx}\:={u}\:\Rightarrow{x}\:={sinu}\:\Rightarrow{tan}\left({arcsinx}\right)\:={tanu} \\ $$$$=\frac{{sinu}}{{cosu}}\:=\frac{{sinu}}{\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {u}}}\:=\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Commented by Ar Brandon last updated on 12/May/20
Thanks Mathmax ��
Commented by mathmax by abdo last updated on 12/May/20
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by hknkrc46 last updated on 12/May/20
i) arctan x=u ⇒ tan u=x ∧ cos u=h=? tan u=((sin u)/(cos u))=((√(1−cos^2 u))/(cos u))=((√(1−h^2 ))/h)=x ⇒ (√(1−h^2 ))=hx ⇒ 1−h^2 =h^2 x^2 ⇒ h^2 x^2 +h^2 =1 ⇒ h^2 (x^2 +1)=1 ⇒ h^2 =(1/(x^2 +1)) ⇒ h=(1/( (√(x^2 +1)))) ii) arcsin x=u ⇒ sin u=x ∧ cos u=? cos u=(√(cos^2 u))=(√(1−sin^2 u))=(√(1−x^2 )) iii) arcsin x=u ⇒ sin u=x ∧ tan u=h=? h=tan u=((sin u)/(cos u))=((sin u)/( (√(1−sin^2 u))))=(x/( (√(1−x^2 ))))
$$\left.{i}\right)\:\mathrm{arctan}\:{x}={u}\:\Rightarrow\:\mathrm{tan}\:{u}={x}\:\wedge\:\mathrm{cos}\:{u}={h}=? \\ $$$$\mathrm{tan}\:{u}=\frac{\mathrm{sin}\:{u}}{\mathrm{cos}\:{u}}=\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {u}}}{\mathrm{cos}\:{u}}=\frac{\sqrt{\mathrm{1}−{h}^{\mathrm{2}} }}{{h}}={x} \\ $$$$\Rightarrow\:\sqrt{\mathrm{1}−{h}^{\mathrm{2}} }={hx}\:\Rightarrow\:\mathrm{1}−{h}^{\mathrm{2}} ={h}^{\mathrm{2}} {x}^{\mathrm{2}} \\ $$$$\Rightarrow\:{h}^{\mathrm{2}} {x}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:{h}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow\:{h}^{\mathrm{2}} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\:{h}=\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\left.{ii}\right)\:\mathrm{arcsin}\:{x}={u}\:\Rightarrow\:\mathrm{sin}\:{u}={x}\:\wedge\:\mathrm{cos}\:{u}=? \\ $$$$\mathrm{cos}\:{u}=\sqrt{\mathrm{cos}\:^{\mathrm{2}} {u}}=\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {u}}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\left.{iii}\right)\:\mathrm{arcsin}\:{x}={u}\:\Rightarrow\:\mathrm{sin}\:{u}={x}\:\wedge\:\mathrm{tan}\:{u}={h}=? \\ $$$${h}=\mathrm{tan}\:{u}=\frac{\mathrm{sin}\:{u}}{\mathrm{cos}\:{u}}=\frac{\mathrm{sin}\:{u}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {u}}}=\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Commented by Ar Brandon last updated on 12/May/20
hknkrc46 Thank you sir ��
Answered by Rio Michael last updated on 12/May/20
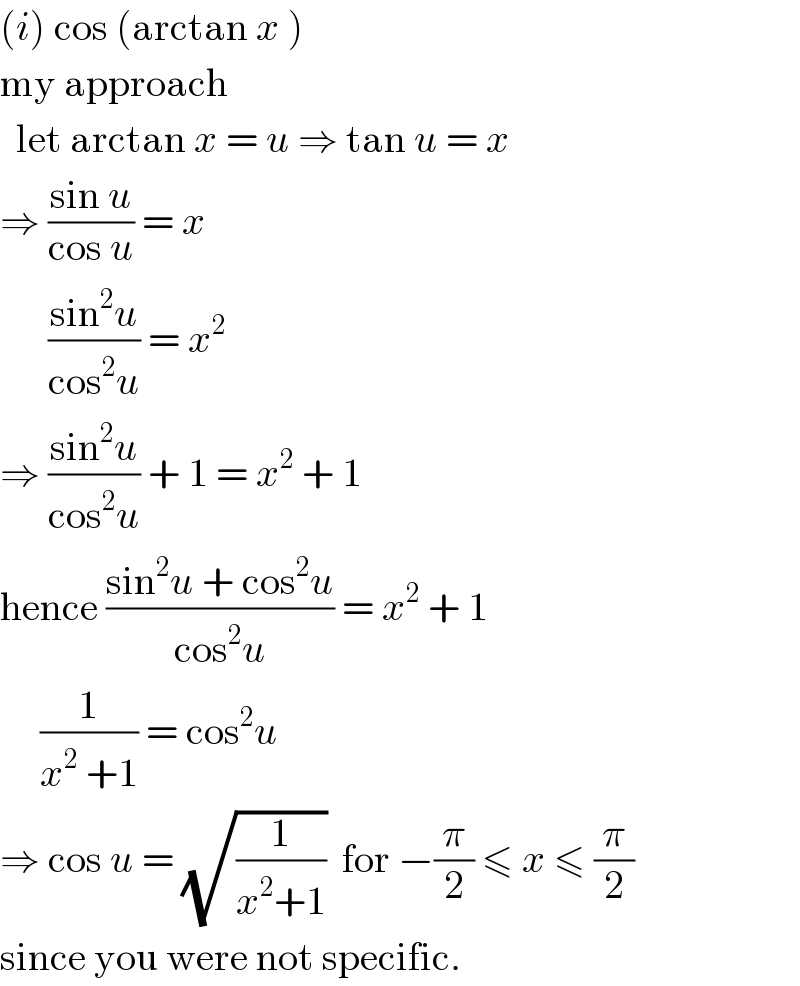
(i) cos (arctan x ) my approach let arctan x = u ⇒ tan u = x ⇒ ((sin u)/(cos u)) = x ((sin^2 u)/(cos^2 u)) = x^2 ⇒ ((sin^2 u)/(cos^2 u)) + 1 = x^2 + 1 hence ((sin^2 u + cos^2 u)/(cos^2 u)) = x^2 + 1 (1/(x^2 +1)) = cos^2 u ⇒ cos u = (√(1/(x^2 +1))) for −(π/2) ≤ x ≤ (π/2) since you were not specific.
$$\left({i}\right)\:\mathrm{cos}\:\left(\mathrm{arctan}\:{x}\:\right) \\ $$$$\mathrm{my}\:\mathrm{approach} \\ $$$$\:\:\mathrm{let}\:\mathrm{arctan}\:{x}\:=\:{u}\:\Rightarrow\:\mathrm{tan}\:{u}\:=\:{x} \\ $$$$\Rightarrow\:\frac{\mathrm{sin}\:{u}}{\mathrm{cos}\:{u}}\:=\:{x} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{sin}^{\mathrm{2}} {u}}{\mathrm{cos}^{\mathrm{2}} {u}}\:=\:{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{sin}^{\mathrm{2}} {u}}{\mathrm{cos}^{\mathrm{2}} {u}}\:+\:\mathrm{1}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$\mathrm{hence}\:\frac{\mathrm{sin}^{\mathrm{2}} {u}\:+\:\mathrm{cos}^{\mathrm{2}} {u}}{\mathrm{cos}^{\mathrm{2}} {u}}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\:\mathrm{cos}^{\mathrm{2}} {u} \\ $$$$\Rightarrow\:\mathrm{cos}\:{u}\:=\:\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}}\:\:\mathrm{for}\:−\frac{\pi}{\mathrm{2}}\:\leqslant\:{x}\:\leqslant\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{since}\:\mathrm{you}\:\mathrm{were}\:\mathrm{not}\:\mathrm{specific}. \\ $$
Commented by Ar Brandon last updated on 12/May/20
Thanks Mr Rio Michael. Good Day Sir ��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *