Menu Close

calculate-I-n-0-1-x-n-1-x-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 82439 by mathmax by abdo last updated on 21/Feb/20
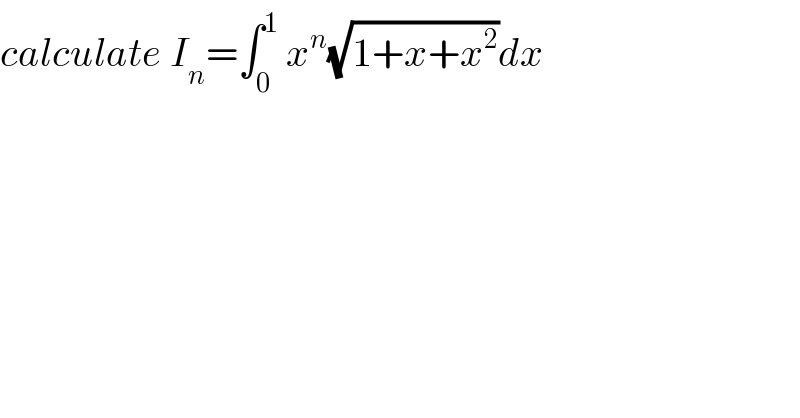
calculate I_n =∫_0 ^1 x^n (√(1+x+x^2 ))dx
$${calculate}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx} \\ $$
Commented by abdomathmax last updated on 24/Feb/20
I_n =∫_0 ^1 x^n (√(1+x+x^2 ))dx =∫_0 ^1 x^n (√((x+(1/2))^2 +(3/4)))dx changement x+(1/2)=((√3)/2)sh(t) give ((2x+1)/( (√3)))=sh(t) ⇒ t argsh(((2x+1)/( (√3))))=ln(((2x+1)/( (√3)))+(√(1+(((2x+1)/( (√3))))^2 ))) ⇒ I_n = ∫_(ln((1/( (√3)))+(√(4/3)))) ^(ln((√3)+2)) (((√3)/2)sh(t)−(1/2))^n ×((√3)/2)ch(t)((√3)/2)ch(t)dt =(1/2^(n+2) ) ∫_(ln((√3))) ^(ln(2+(√3))) ((√3)sh(t)−1)^n ch^2 t dt =(1/2^(n+2) ) ∫_(ln((√3))) ^(ln(2+(√3))) (Σ_(k=0) ^n C_n ^k ((√3)sh(t))^k (−1)^(n−k) )×((1+ch(2t))/2)dt =(1/2^(n+3) )Σ_(k=0) ^n C_n ^k ((√3))^(k ) ∫_(ln((√3))) ^(ln(2+(√3))) sh^k (t)(−1)^(n−k) (1+ch(2t))dt ...be continued...
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}{dx} \\ $$$${changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:{give}\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}={sh}\left({t}\right)\:\Rightarrow \\ $$$${t}\: \\ $$$${argsh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)={ln}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${I}_{{n}} =\:\int_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\frac{\mathrm{4}}{\mathrm{3}}}\right)} ^{{ln}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} ×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{2}} }\:\int_{{ln}\left(\sqrt{\mathrm{3}}\right)} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \left(\sqrt{\mathrm{3}}{sh}\left({t}\right)−\mathrm{1}\right)^{{n}} \:{ch}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{2}} }\:\int_{{ln}\left(\sqrt{\mathrm{3}}\right)} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(\sqrt{\mathrm{3}}{sh}\left({t}\right)\right)^{{k}} \left(−\mathrm{1}\right)^{{n}−{k}} \right)×\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{3}} }\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(\sqrt{\mathrm{3}}\right)^{{k}\:} \int_{{ln}\left(\sqrt{\mathrm{3}}\right)} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} {sh}^{{k}} \left({t}\right)\left(−\mathrm{1}\right)^{{n}−{k}} \left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *