Menu Close

Calculate-If-0-1-tanh-1-x-3-x-dx-2-then-M-N-

Tinku Tara 0 Comments
Pin




Question Number 166690 by mnjuly1970 last updated on 25/Feb/22
Calculate If , 𝛗= ∫_0 ^( 1) (( tanh^( βˆ’1) ( x^( 3) ))/x) dx = Ξ±.ΞΆ( 2) then , Ξ± = ? β–  M.N βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’
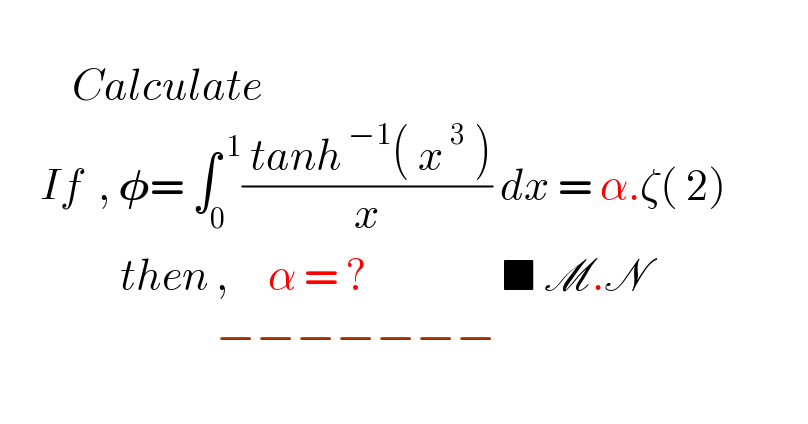
$$ \\ $$$$\:\:\:\:\:\:\:\:\:{Calculate}\: \\ $$$$\:\:\:\:\:{If}\:\:,\:\boldsymbol{\phi}=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{tanh}^{\:βˆ’\mathrm{1}} \left(\:{x}^{\:\mathrm{3}} \:\right)}{{x}}\:{dx}\:=\:\alpha.\zeta\left(\:\mathrm{2}\right)\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{then}\:,\:\:\:\:\:\alpha\:=\:?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare\:\mathscr{M}.\mathscr{N}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’ \\ $$$$ \\ $$
Answered by amin96 last updated on 25/Feb/22
solution: x^3 =t (dt/dx)=3x^2 =3t^(2/3) dx=(dt/(3t^(2/3) )) 𝛗=(1/3)∫_0 ^1 ((arctgh(t))/t)dt=(1/6)∫_0 ^1 ((ln(((1+t)/(1βˆ’t))))/t)dt= =(1/6)∫_0 ^1 (1/t)ln(((1+t)/(1βˆ’t)))dt=(1/3)∫_0 ^1 (1/t)Ξ£_(n=0) ^∞ (t^(2n+1) /(2n+1))dt= =(1/3)Ξ£_(n=0) ^∞ (1/(2n+1))∫_0 ^1 t^(2n) dt=(1/3)Ξ£_(n=0) ^∞ (1/((2n+1)^2 ))= =(1/3)(1+(1/3^2 )+(1/5^2 )+(1/7^2 )+…)=(1/3)(𝛇(2)βˆ’(1/4)𝛇(2))= =(1/4)𝛇(2) 𝛂=(1/4) by M.A
$$\underline{\boldsymbol{\mathrm{solution}}:}\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} =\boldsymbol{\mathrm{t}}\:\:\:\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{dx}}}=\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\mathrm{3}\boldsymbol{\mathrm{t}}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\:\:\:\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{dt}}}{\mathrm{3}\boldsymbol{\mathrm{t}}^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\boldsymbol{\phi}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{arctgh}}\left(\boldsymbol{\mathrm{t}}\right)}{\boldsymbol{\mathrm{t}}}\boldsymbol{\mathrm{dt}}=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}+\boldsymbol{\mathrm{t}}}{\mathrm{1}βˆ’\boldsymbol{\mathrm{t}}}\right)}{\boldsymbol{\mathrm{t}}}\boldsymbol{\mathrm{dt}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}}\boldsymbol{\mathrm{ln}}\left(\frac{\mathrm{1}+\boldsymbol{\mathrm{t}}}{\mathrm{1}βˆ’\boldsymbol{\mathrm{t}}}\right)\boldsymbol{\mathrm{dt}}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\boldsymbol{\mathrm{t}}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\mathrm{t}}^{\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}} }{\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}}\boldsymbol{\mathrm{dt}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{t}}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \boldsymbol{\mathrm{dt}}=\frac{\mathrm{1}}{\mathrm{3}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+\ldots\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\boldsymbol{\zeta}\left(\mathrm{2}\right)βˆ’\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\zeta}\left(\mathrm{2}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\zeta}\left(\mathrm{2}\right)\:\:\:\:\:\boldsymbol{\alpha}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{by}}\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$
Commented by mnjuly1970 last updated on 25/Feb/22
grateful sir Amin ...excellent
$${grateful}\:{sir}\:{Amin}\:…{excellent} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *