Question Number 160372 by LEKOUMA last updated on 28/Nov/21
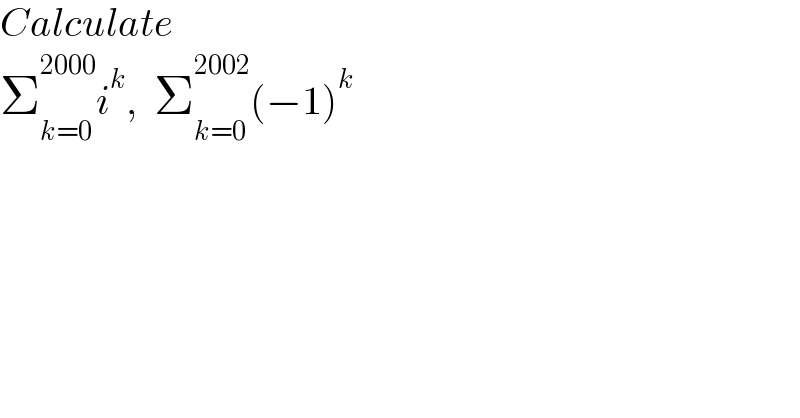
$${Calculate} \\ $$$$\sum_{{k}=\mathrm{0}} ^{\mathrm{2000}} {i}^{{k}} ,\:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2002}} \left(−\mathrm{1}\right)^{{k}} \\ $$
Answered by mathmax by abdo last updated on 28/Nov/21
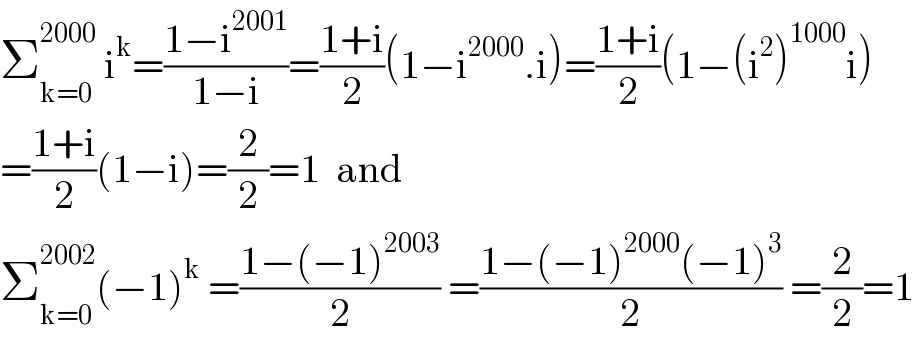
$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2000}} \:\mathrm{i}^{\mathrm{k}} =\frac{\mathrm{1}−\mathrm{i}^{\mathrm{2001}} }{\mathrm{1}−\mathrm{i}}=\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}^{\mathrm{2000}} .\mathrm{i}\right)=\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\left(\mathrm{1}−\left(\mathrm{i}^{\mathrm{2}} \right)^{\mathrm{1000}} \mathrm{i}\right) \\ $$$$=\frac{\mathrm{1}+\mathrm{i}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\:\:\mathrm{and} \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2002}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:=\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{2003}} }{\mathrm{2}}\:=\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{2000}} \left(−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{2}}\:=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$
