Question Number 55230 by maxmathsup by imad last updated on 19/Feb/19
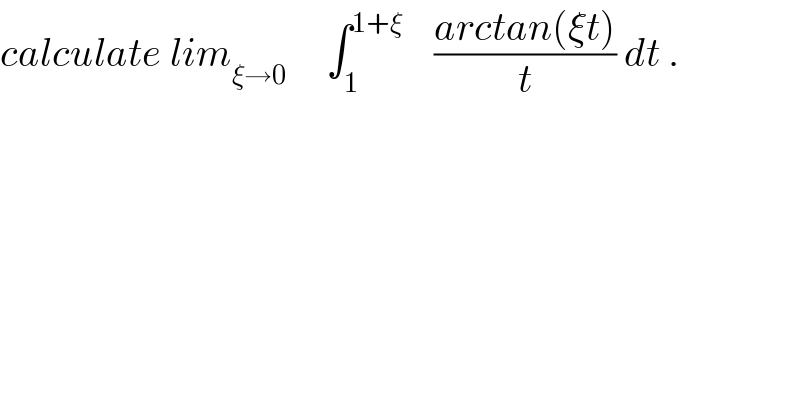
$${calculate}\:{lim}_{\xi\rightarrow\mathrm{0}} \:\:\:\:\:\int_{\mathrm{1}} ^{\mathrm{1}+\xi} \:\:\:\:\frac{{arctan}\left(\xi{t}\right)}{{t}}\:{dt}\:. \\ $$
Commented by maxmathsup by imad last updated on 25/Feb/19
![∃ α ∈]1,1+ξ[ /A(ξ)= ∫_1 ^(1+ξ) ((arctan(ξt))/t) dt = arctan(ξα) ∫_1 ^(1+ξ) (dt/t) =arctan(ξα) ln∣1+ξ∣ ⇒lim_(ξ→0) A(ξ)=arctan(0)ln(1)=0 ⇒ lim_(ξ→0) ∫_1 ^(1+ξ) ((arctan(ξt))/t) dt =0 .](https://www.tinkutara.com/question/Q55513.png)
$$\left.\exists\:\alpha\:\in\right]\mathrm{1},\mathrm{1}+\xi\left[\:/{A}\left(\xi\right)=\:\int_{\mathrm{1}} ^{\mathrm{1}+\xi} \:\frac{{arctan}\left(\xi{t}\right)}{{t}}\:{dt}\:=\:{arctan}\left(\xi\alpha\right)\:\int_{\mathrm{1}} ^{\mathrm{1}+\xi} \:\frac{{dt}}{{t}}\right. \\ $$$$={arctan}\left(\xi\alpha\right)\:{ln}\mid\mathrm{1}+\xi\mid\:\:\:\Rightarrow{lim}_{\xi\rightarrow\mathrm{0}} {A}\left(\xi\right)={arctan}\left(\mathrm{0}\right){ln}\left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{\xi\rightarrow\mathrm{0}} \:\:\int_{\mathrm{1}} ^{\mathrm{1}+\xi} \:\:\frac{{arctan}\left(\xi{t}\right)}{{t}}\:{dt}\:=\mathrm{0}\:. \\ $$
