Question Number 162539 by LEKOUMA last updated on 30/Dec/21
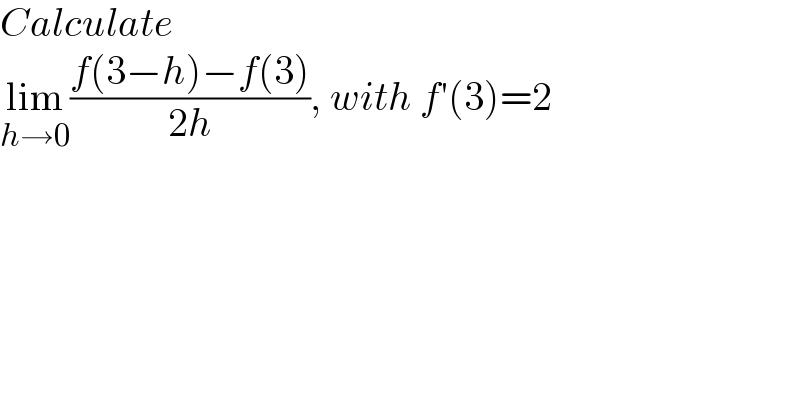
$${Calculate}\: \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}−{h}\right)−{f}\left(\mathrm{3}\right)}{\mathrm{2}{h}},\:{with}\:{f}'\left(\mathrm{3}\right)=\mathrm{2} \\ $$
Answered by Ar Brandon last updated on 30/Dec/21
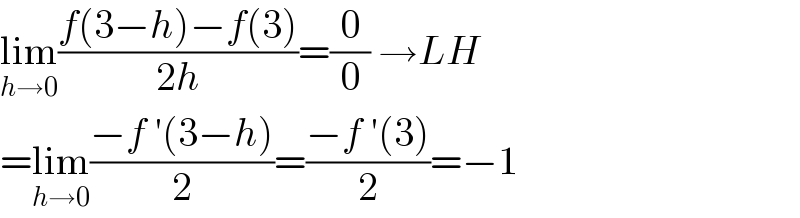
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}−{h}\right)−{f}\left(\mathrm{3}\right)}{\mathrm{2}{h}}=\frac{\mathrm{0}}{\mathrm{0}}\:\rightarrow{LH} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−{f}\:'\left(\mathrm{3}−{h}\right)}{\mathrm{2}}=\frac{−{f}\:'\left(\mathrm{3}\right)}{\mathrm{2}}=−\mathrm{1} \\ $$
Answered by mr W last updated on 30/Dec/21
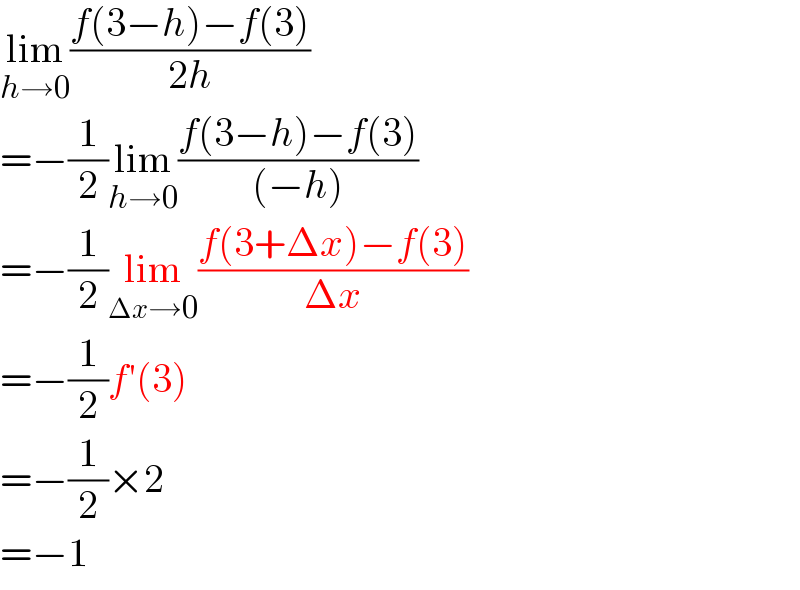
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}−{h}\right)−{f}\left(\mathrm{3}\right)}{\mathrm{2}{h}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}−{h}\right)−{f}\left(\mathrm{3}\right)}{\left(−{h}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}+\Delta{x}\right)−{f}\left(\mathrm{3}\right)}{\Delta{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{f}'\left(\mathrm{3}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2} \\ $$$$=−\mathrm{1} \\ $$
