Question Number 55051 by maxmathsup by imad last updated on 16/Feb/19
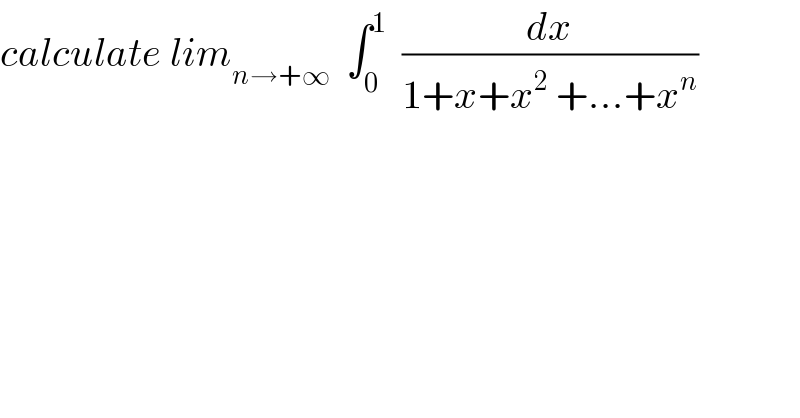
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+…+{x}^{{n}} } \\ $$
Commented by maxmathsup by imad last updated on 24/Feb/19
![let I_n =∫_0 ^1 (dx/(1+x+x^2 +...+x^n )) ⇒I_n =∫_0 ^1 (dx/((1−x^(n+1) )/(1−x))) =∫_0 ^1 ((1−x)/(1−x^(n+1) )) dx =∫_R ((1−x)/(1−x^(n+1) )) χ_(]0,1[) (x) dx the sequence of function f_n (x)=((1−x)/(1−x^(n+1) )) χ_(]0,1[) (x) converges to f(x)=1−x ⇒ im_(n→+∞) I_n =∫_0 ^1 (1−x)dx =[x−(x^2 /2)]_0 ^1 =1−(1/2) =(1/2)](https://www.tinkutara.com/question/Q55453.png)
$${let}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+…+{x}^{{n}} }\:\Rightarrow{I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\frac{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{\mathrm{1}−{x}}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{{n}+\mathrm{1}} }\:{dx} \\ $$$$=\int_{{R}} \:\:\:\:\:\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{{n}+\mathrm{1}} }\:\chi_{\left.\right]\mathrm{0},\mathrm{1}\left[\right.} \left({x}\right)\:{dx}\:\:\:{the}\:{sequence}\:{of}\:{function} \\ $$$${f}_{{n}} \left({x}\right)=\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{{n}+\mathrm{1}} }\:\chi_{\left.\right]\mathrm{0},\mathrm{1}\left[\right.} \left({x}\right)\:\:{converges}\:{to}\:{f}\left({x}\right)=\mathrm{1}−{x}\:\Rightarrow \\ $$$${im}_{{n}\rightarrow+\infty} {I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right){dx}\:=\left[{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
