Question Number 38643 by maxmathsup by imad last updated on 27/Jun/18
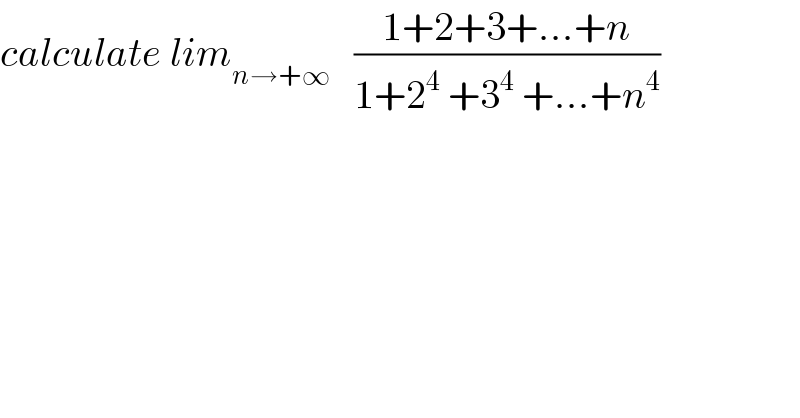
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}}{\mathrm{1}+\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+…+{n}^{\mathrm{4}} } \\ $$
Commented by abdo mathsup 649 cc last updated on 28/Jun/18
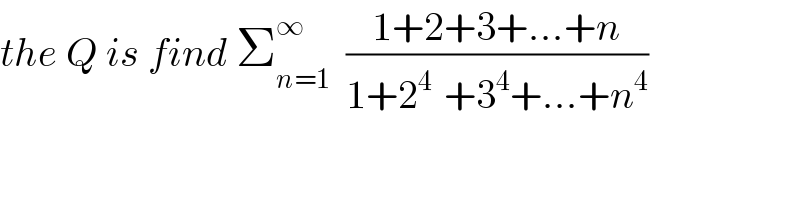
$${the}\:{Q}\:{is}\:{find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}}{\mathrm{1}+\mathrm{2}^{\mathrm{4}\:} \:+\mathrm{3}^{\mathrm{4}} +…+{n}^{\mathrm{4}} } \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18
$${pls}\:{post}\:{the}\:{source}\:{of}\:{the}\:{question}\:{and}\:{validity} \\ $$
Answered by ajfour last updated on 28/Jun/18
![Σ_(r=1) ^n r^4 = Σ_(r=1) ^n r(r+1)(r+2)(r+3) −6Σ_(r=1) ^n r^3 −11Σ_(r=1) ^n r^2 −6Σ_(r=1) ^n r =((n(n+1)(n+2)(n+3)(n+4))/5) −((6n^2 (n+1)^2 )/4)−((11n(n+1)(2n+1))/6) −((6n(n+1))/2) = ((n(n+1))/(30)){6(n+2)(n+3)(n+4) −45n(n+1)−55(2n+1)−90} =((n(n+1))/(30)){6n^3 +9n^2 +6n−1} So lim_(n→∞) (((Σ_(r=1) ^n r)^(5/2) )/(Σ_(r=1) ^n r^4 )) = lim_(n→∞) (([((n(n+1))/2)]^(5/2) )/([((n(n+1))/(30))(6n^3 +9n^2 +6n−1)])) =((((1/2))^(5/2) )/(((1/(30)))×6)) = (5/(4(√2))) .](https://www.tinkutara.com/question/Q38652.png)
$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{4}} \:=\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\left({r}+\mathrm{1}\right)\left({r}+\mathrm{2}\right)\left({r}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{3}} −\mathrm{11}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{2}} −\mathrm{6}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\left({n}+\mathrm{4}\right)}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:−\frac{\mathrm{6}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{11}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:−\frac{\mathrm{6}{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{30}}\left\{\mathrm{6}\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\left({n}+\mathrm{4}\right)\right. \\ $$$$\left.\:\:\:\:−\mathrm{45}{n}\left({n}+\mathrm{1}\right)−\mathrm{55}\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{90}\right\} \\ $$$$\:\:\:=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{30}}\left\{\mathrm{6}{n}^{\mathrm{3}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{6}{n}−\mathrm{1}\right\} \\ $$$${So}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\right)^{\mathrm{5}/\mathrm{2}} }{\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{4}} }\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right]^{\mathrm{5}/\mathrm{2}} }{\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{30}}\left(\mathrm{6}{n}^{\mathrm{3}} +\mathrm{9}{n}^{\mathrm{2}} +\mathrm{6}{n}−\mathrm{1}\right)\right]} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{5}/\mathrm{2}} }{\left(\frac{\mathrm{1}}{\mathrm{30}}\right)×\mathrm{6}}\:=\:\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{2}}}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

$${why}\:\left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 28/Jun/18

$${I}\:{did}\:{not}\:{like}\:{the}\:{obvious}\:{answer} \\ $$$${to}\:{the}\:{original}\:{question},\:{so}\:{i} \\ $$$${changed}\:{the}\:{question}\:!\left(\overset{\hat {°}\:\:\:\:\:\:\:\hat {°}\:} {\smile}\right)! \\ $$
