Menu Close

calculate-lim-n-1-2i-1-it-n-n-1-it-n-n-

Tinku Tara 0 Comments
Pin




Question Number 36924 by maxmathsup by imad last updated on 07/Jun/18
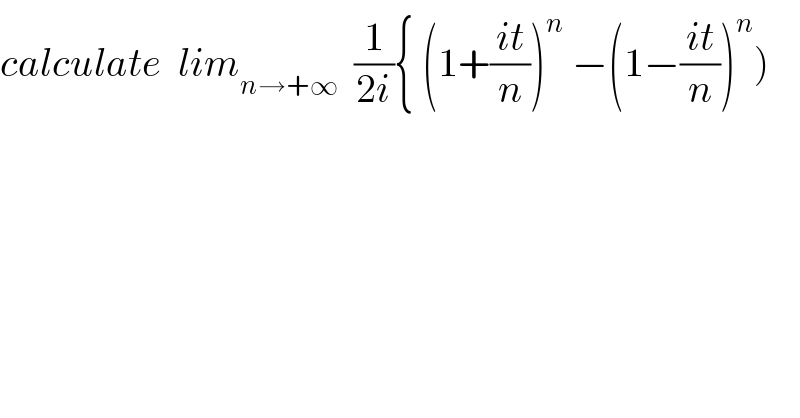
calculate lim_(n→+∞) (1/(2i)){ (1+((it)/n))^n −(1−((it)/n))^n )
$${calculate}\:\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\:\left(\mathrm{1}+\frac{{it}}{{n}}\right)^{{n}} \:−\left(\mathrm{1}−\frac{{it}}{{n}}\right)^{{n}} \right) \\ $$
Commented by math khazana by abdo last updated on 09/Jun/18
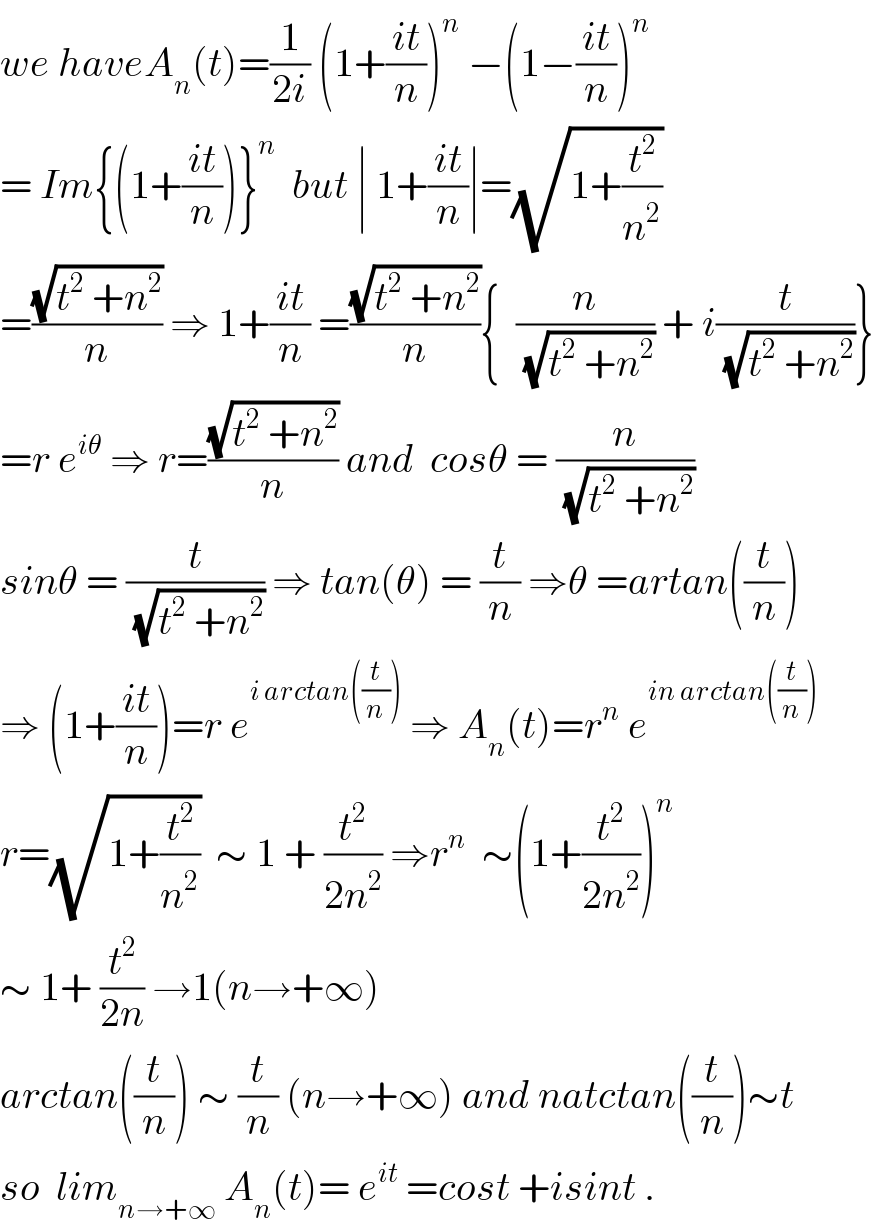
we haveA_n (t)=(1/(2i)) (1+((it)/n))^n −(1−((it)/n))^n = Im{(1+((it)/n))}^n but ∣ 1+((it)/n)∣=(√(1+(t^2 /n^2 ))) =((√(t^2 +n^2 ))/n) ⇒ 1+((it)/n) =((√(t^2 +n^2 ))/n){ (n/( (√(t^2 +n^2 )))) + i(t/( (√(t^2 +n^2 ))))} =r e^(iθ) ⇒ r=((√(t^2 +n^2 ))/n) and cosθ = (n/( (√(t^2 +n^2 )))) sinθ = (t/( (√(t^2 +n^2 )))) ⇒ tan(θ) = (t/n) ⇒θ =artan((t/n)) ⇒ (1+((it)/n))=r e^(i arctan((t/n))) ⇒ A_n (t)=r^n e^(in arctan((t/n))) r=(√(1+(t^2 /n^2 ))) ∼ 1 + (t^2 /(2n^2 )) ⇒r^n ∼(1+(t^2 /(2n^2 )))^n ∼ 1+ (t^2 /(2n)) →1(n→+∞) arctan((t/n)) ∼ (t/n) (n→+∞) and natctan((t/n))∼t so lim_(n→+∞) A_n (t)= e^(it) =cost +isint .
$${we}\:{haveA}_{{n}} \left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\:\left(\mathrm{1}+\frac{{it}}{{n}}\right)^{{n}} \:−\left(\mathrm{1}−\frac{{it}}{{n}}\right)^{{n}} \\ $$$$=\:{Im}\left\{\left(\mathrm{1}+\frac{{it}}{{n}}\right)\right\}^{{n}} \:\:{but}\:\mid\:\mathrm{1}+\frac{{it}}{{n}}\mid=\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }} \\ $$$$=\frac{\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}{{n}}\:\Rightarrow\:\mathrm{1}+\frac{{it}}{{n}}\:=\frac{\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}{{n}}\left\{\:\:\frac{{n}}{\:\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}\:+\:{i}\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}\right\} \\ $$$$={r}\:{e}^{{i}\theta} \:\Rightarrow\:{r}=\frac{\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}{{n}}\:{and}\:\:{cos}\theta\:=\:\frac{{n}}{\:\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }} \\ $$$${sin}\theta\:=\:\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}\:\Rightarrow\:{tan}\left(\theta\right)\:=\:\frac{{t}}{{n}}\:\Rightarrow\theta\:={artan}\left(\frac{{t}}{{n}}\right) \\ $$$$\Rightarrow\:\left(\mathrm{1}+\frac{{it}}{{n}}\right)={r}\:{e}^{{i}\:{arctan}\left(\frac{{t}}{{n}}\right)} \:\Rightarrow\:{A}_{{n}} \left({t}\right)={r}^{{n}} \:{e}^{{in}\:{arctan}\left(\frac{{t}}{{n}}\right)} \\ $$$${r}=\sqrt{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\:\sim\:\mathrm{1}\:+\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\:\Rightarrow{r}^{{n}} \:\:\sim\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\right)^{{n}} \\ $$$$\sim\:\mathrm{1}+\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}{n}}\:\rightarrow\mathrm{1}\left({n}\rightarrow+\infty\right) \\ $$$${arctan}\left(\frac{{t}}{{n}}\right)\:\sim\:\frac{{t}}{{n}}\:\left({n}\rightarrow+\infty\right)\:{and}\:{natctan}\left(\frac{{t}}{{n}}\right)\sim{t} \\ $$$${so}\:\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \left({t}\right)=\:{e}^{{it}} \:={cost}\:+{isint}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *