Question Number 40759 by math khazana by abdo last updated on 27/Jul/18

$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\:\:\frac{\mathrm{1}−{e}^{−{nx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} {sin}\left(\frac{\pi}{{n}}\right)} \\ $$
Commented by math khazana by abdo last updated on 27/Jul/18

$${the}\:{Q}\:{is}\:{find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{1}−{e}^{−{nx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:{sin}\left(\frac{\pi{x}}{{n}}\right)} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18
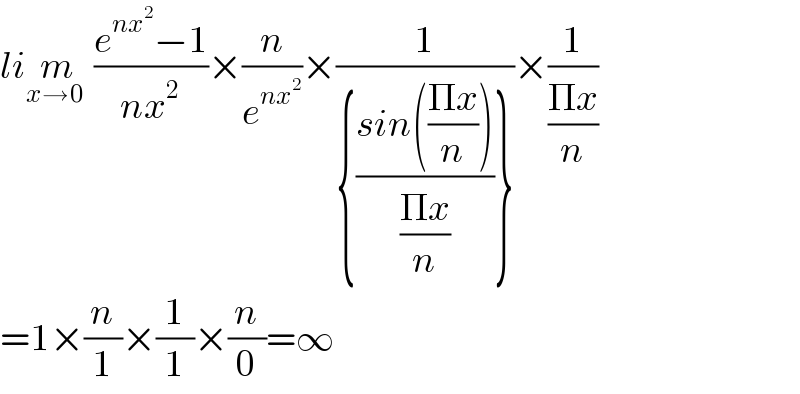
$${li}\underset{{x}\rightarrow\mathrm{0}\:} {{m}}\:\frac{{e}^{{nx}^{\mathrm{2}} } −\mathrm{1}}{{nx}^{\mathrm{2}} }×\frac{{n}}{{e}^{{nx}^{\mathrm{2}} } }×\frac{\mathrm{1}}{\left\{\frac{{sin}\left(\frac{\Pi{x}}{{n}}\right)}{\frac{\Pi{x}}{{n}}}\right\}}×\frac{\mathrm{1}}{\frac{\Pi{x}}{{n}}} \\ $$$$=\mathrm{1}×\frac{{n}}{\mathrm{1}}×\frac{\mathrm{1}}{\mathrm{1}}×\frac{{n}}{\mathrm{0}}=\infty \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18

$${li}\underset{{n}\rightarrow\infty} {{m}}\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{{e}^{{nx}^{\mathrm{2}} } }}{{x}^{\mathrm{2}} {sin}\left(\frac{\Pi}{{n}}\right)} \\ $$$${when}\:\:{n}\rightarrow\infty\:\:\frac{\mathrm{1}}{{e}^{{nx}^{\mathrm{2}} } }\:\rightarrow\mathrm{0}\:\:\:{and}\:{for}\:{any}\:{value}\:{of} \\ $$$${n}\:\:{the}\:{value}\:{of}\:{sin}\left(\frac{\Pi}{{n}}\right)\:{lies}\:{between}\:\pm\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }>\:\:{li}\underset{{n}\rightarrow\infty} {{m}}\:\:\frac{\mathrm{1}−{e}^{−{nx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} {sin}\left(\frac{\Pi}{{n}}\right)}>−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$
