Question Number 111771 by mathmax by abdo last updated on 04/Sep/20
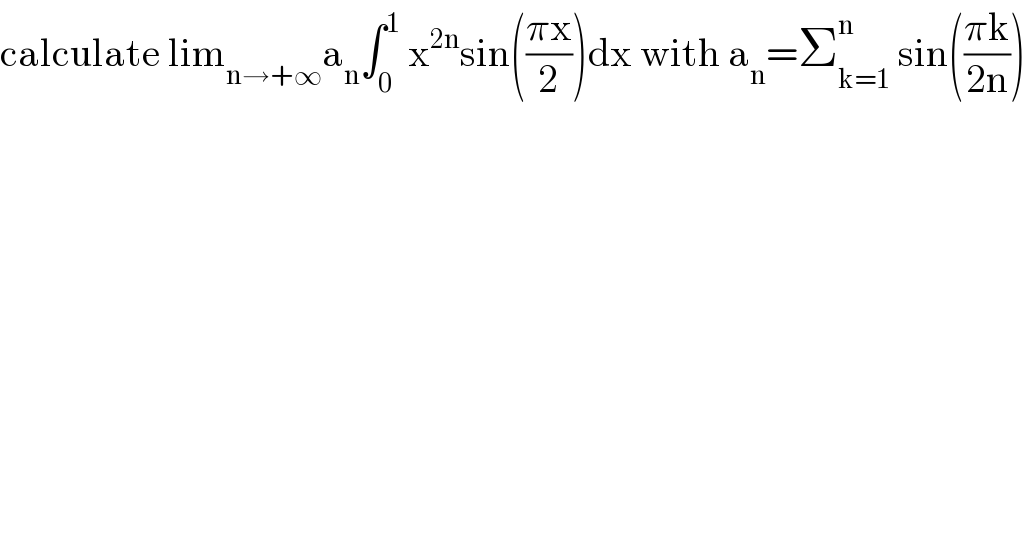
$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{a}_{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{sin}\left(\frac{\pi\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx}\:\mathrm{with}\:\mathrm{a}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{sin}\left(\frac{\pi\mathrm{k}}{\mathrm{2n}}\right) \\ $$
