Question Number 62877 by mathmax by abdo last updated on 26/Jun/19
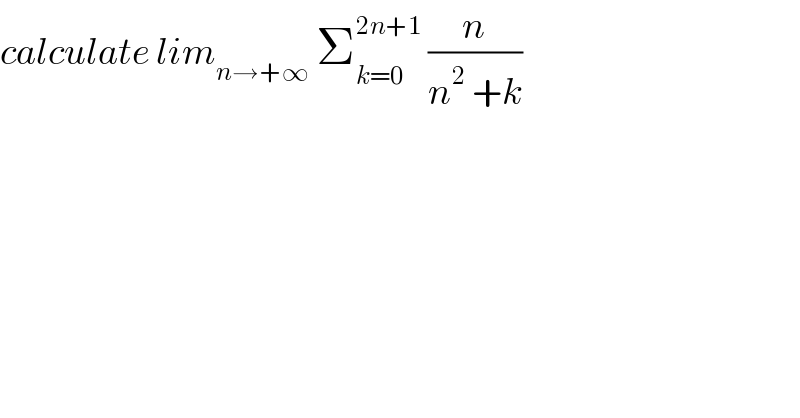
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}+\mathrm{1}} \:\frac{{n}}{{n}^{\mathrm{2}} \:+{k}} \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
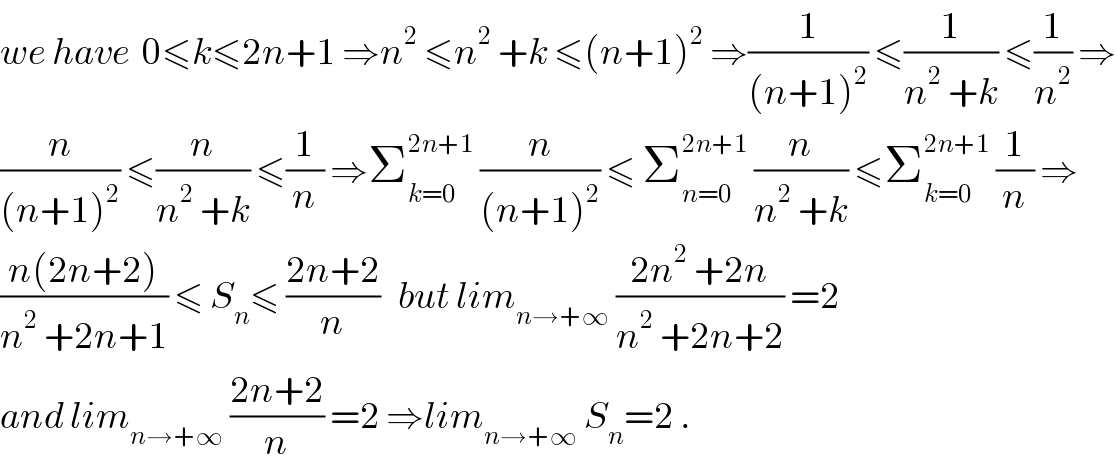
$${we}\:{have}\:\:\mathrm{0}\leqslant{k}\leqslant\mathrm{2}{n}+\mathrm{1}\:\Rightarrow{n}^{\mathrm{2}} \:\leqslant{n}^{\mathrm{2}} \:+{k}\:\leqslant\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+{k}}\:\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{{n}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\leqslant\frac{{n}}{{n}^{\mathrm{2}} \:+{k}}\:\leqslant\frac{\mathrm{1}}{{n}}\:\Rightarrow\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}+\mathrm{1}} \:\frac{{n}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\leqslant\:\sum_{{n}=\mathrm{0}} ^{\mathrm{2}{n}+\mathrm{1}} \:\frac{{n}}{{n}^{\mathrm{2}} \:+{k}}\:\leqslant\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{n}}\:\Rightarrow \\ $$$$\frac{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)}{{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{1}}\:\leqslant\:{S}_{{n}} \leqslant\:\frac{\mathrm{2}{n}+\mathrm{2}}{{n}}\:\:\:{but}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{2}{n}}{{n}^{\mathrm{2}} \:+\mathrm{2}{n}+\mathrm{2}}\:=\mathrm{2} \\ $$$${and}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{2}{n}+\mathrm{2}}{{n}}\:=\mathrm{2}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\mathrm{2}\:. \\ $$
