Question Number 111754 by mathmax by abdo last updated on 04/Sep/20
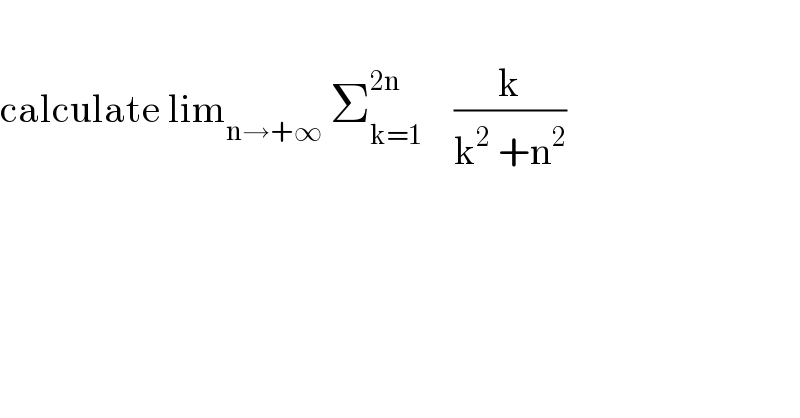
$$ \\ $$$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \:\:\:\:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 04/Sep/20
![lim_(n→∞) (1/n)Σ^(2n) (k/((k^2 /n)+n))=lim_(n→∞) (1/n)Σ_(k=1) ^(2n) (1/((k/n)+(n/k)))=∫_0 ^2 (1/(x+(1/x)))dx =(1/2)∫_0 ^2 ((2x)/(x^2 +1))dx =[(1/2)log(x^2 +1)]_0 ^2 =(1/2)log(5)](https://www.tinkutara.com/question/Q111758.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\overset{\mathrm{2}{n}} {\sum}\frac{{k}}{\frac{{k}^{\mathrm{2}} }{{n}}+{n}}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\frac{\mathrm{1}}{\frac{{k}}{{n}}+\frac{{n}}{{k}}}=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{5}\right) \\ $$
Answered by mathmax by abdo last updated on 07/Sep/20
![A_n =Σ_(k=1) ^n (k/(k^2 +n^2 )) +Σ_(k=n+1) ^(2n) (k/(k^2 +n^2 )) =S_1 ^n + S_2 ^n S_1 ^n =Σ_(k=1) ^n (k/(k^2 (1+(n^2 /k^2 )))) =(1/n)Σ_(k=1) ^n (n/(k(1+(1/(n^2 /k^2 ))))) →∫_0 ^1 (x/(1+(1/x)))dx =∫_0 ^1 (x^2 /(x+1))dx =∫_0 ^1 ((x^2 −1+1)/(x+1)) dx =∫_0 ^1 (x−1)dx +∫_0 ^1 (dx/(x+1)) =[(x^2 /2)−x]_0 ^1 +[ln(x+1)]_0 ^1 =−(1/2) +ln(2) S_2 ^n =Σ_(k=n+1) ^(2n) (k/(k^2 +n^2 )) =_(k−n=p) Σ_(p=1) ^n ((n+p)/((n+p)^2 +n^2 )) =Σ_(p=1) ^n ((n+p)/(n^2 +2np +p^2 +n^2 )) =Σ_(p=1) ^n ((n+p)/(2n^2 +2np +p^2 )) =Σ_(p=1) ^n ((n(1+(p/n)))/(n^2 (2 +((2p)/n)+(p^2 /n^2 )))) =(1/n) Σ_(p=1) ^n ((1+(p/n))/(((p/n))^2 +2((p/n))+2))→∫_0 ^(1 ) ((1+x)/(x^2 +2x +2))dx =(1/2) ∫_0 ^1 ((2x+2)/(x^2 +2x+2)) dx =(1/2)[ln(x^2 +2x+2)]_0 ^1 =(1/2)(ln(5)−ln(2)) ⇒ lim_(n→+∞) A_n =ln(2)−(1/2) +(1/2)ln5 −(1/2)ln2 =(1/2)ln2+(1/2)ln5−(1/2) =ln((√(10)))−(1/2)](https://www.tinkutara.com/question/Q112265.png)
$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }\:+\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\mathrm{2n}} \:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }\:=\mathrm{S}_{\mathrm{1}} ^{\mathrm{n}} \:+\:\mathrm{S}_{\mathrm{2}} ^{\mathrm{n}} \\ $$$$\mathrm{S}_{\mathrm{1}} ^{\mathrm{n}} \:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}}{\mathrm{k}\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{k}^{\mathrm{2}} }}\right)}\:\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}−\mathrm{1}\right)\mathrm{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{1}} \\ $$$$=\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\left[\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{S}_{\mathrm{2}} ^{\mathrm{n}} \:=\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\mathrm{2n}} \:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }\:=_{\mathrm{k}−\mathrm{n}=\mathrm{p}} \:\:\sum_{\mathrm{p}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}+\mathrm{p}}{\left(\mathrm{n}+\mathrm{p}\right)^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{p}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}+\mathrm{p}}{\mathrm{n}^{\mathrm{2}} +\mathrm{2np}\:+\mathrm{p}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }\:=\sum_{\mathrm{p}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}+\mathrm{p}}{\mathrm{2n}^{\mathrm{2}} \:+\mathrm{2np}\:+\mathrm{p}^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{p}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}\left(\mathrm{1}+\frac{\mathrm{p}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} \left(\mathrm{2}\:+\frac{\mathrm{2p}}{\mathrm{n}}+\frac{\mathrm{p}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{p}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}+\frac{\mathrm{p}}{\mathrm{n}}}{\left(\frac{\mathrm{p}}{\mathrm{n}}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\frac{\mathrm{p}}{\mathrm{n}}\right)+\mathrm{2}}\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{1}+\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}\:+\mathrm{2}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\left(\mathrm{5}\right)−\mathrm{ln}\left(\mathrm{2}\right)\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln5}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{ln}\left(\sqrt{\mathrm{10}}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
