Question Number 129869 by Bird last updated on 20/Jan/21
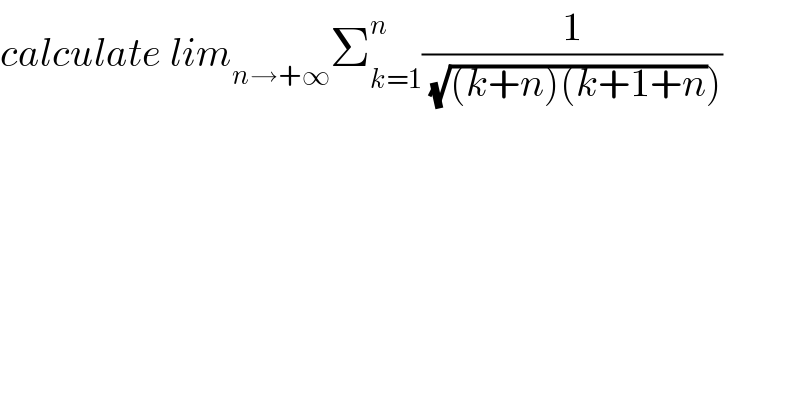
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{\left.\:\sqrt{\left({k}+{n}\right)\left({k}+\mathrm{1}+{n}\right.}\right)} \\ $$
Answered by mindispower last updated on 20/Jan/21

$$ \\ $$$$\frac{\mathrm{1}}{\left({k}+\mathrm{1}+{n}\right)}\leqslant\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}.\sqrt{{k}+\mathrm{1}+{n}}}\leqslant\frac{\mathrm{1}}{{k}+{n}}…\mathrm{1} \\ $$$$\Sigma\frac{\mathrm{1}}{{k}+{n}}=\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{n}}.\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}={ln}\left(\mathrm{2}\right) \\ $$$$\underset{{k}\leqslant{n}} {\sum}\left(\frac{\mathrm{1}}{{k}+{n}}−\frac{\mathrm{1}}{{k}+\mathrm{1}+{n}}\right)=\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{\left({k}+{n}\right)\left({k}+\mathrm{1}+{n}\right)}={T} \\ $$$${T}\leqslant\underset{{k}\leqslant{n}} {\sum}.\frac{\mathrm{1}}{\left(\mathrm{1}+{n}\right)\left({k}+{n}\right)}\leqslant\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}=\frac{{n}}{{n}\left({n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{n}+\mathrm{1}}\rightarrow\mathrm{0} \\ $$$$\Rightarrow\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{\left({k}+{n}\right)}−\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{\left({k}+\mathrm{1}+{n}\right)}\rightarrow\mathrm{0} \\ $$$${since}\:\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{\left({k}+{n}\right)}\rightarrow{ln}\left(\mathrm{2}\right)\Rightarrow\Sigma\frac{\mathrm{1}}{{k}+\mathrm{1}+{n}}\rightarrow{ln}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\Sigma\frac{\mathrm{1}}{\:\sqrt{{k}+{n}.}.\sqrt{{k}+\mathrm{1}+{n}}}\rightarrow{ln}\left(\mathrm{2}\right)\:{by}\:{using}\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
