Question Number 111772 by mathmax by abdo last updated on 04/Sep/20
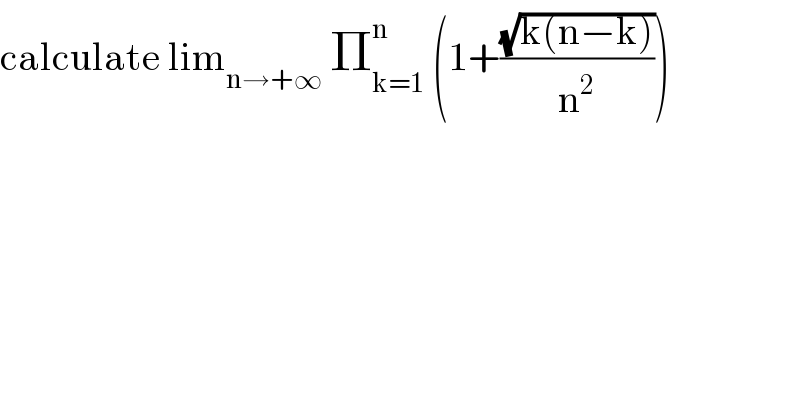
$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\mathrm{1}+\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$
Answered by mathmax by abdo last updated on 07/Sep/20
![let A_n =Π_(k=1) ^n (1+((√(k(n−k)))/n^2 )) ⇒ln(A_n ) =Σ_(k=1) ^n ln(1+((√(k(n−k)))/n^2 )) we have (d/dx)ln(1+x) =(1/(1+x)) =1−x +x^2 −...for ∣x∣<1 ⇒ ln(1+x) =x−(x^2 /2) +(x^3 /3)−... ⇒x−(x^2 /2)≤ln(1+x)≤x ⇒ ((√(k(n−k)))/n^2 )−((k(n−k))/n^4 ) ≤ln(1+((√(k(n−k)))/n^2 ))≤((√(k(n−k)))/n^2 ) ⇒ (1/n^2 )Σ_(k=1) ^n (√(k(n−k)))−(1/n^4 ) Σ_(k=1) ^n k(n−k)≤ln(A_n )≤(1/n^2 ) Σ_(k=1) ^n (√(k(n−k))) (1/n^4 ) Σ_(k=1) ^(n ) (nk−k^2 ) =(1/n^3 ) Σ_(k=1) ^n k −(1/n^4 ) Σ_(k=1) ^n k^2 =(1/n^3 )×((n(n+1))/2)−(1/n^4 )((n(n+1)(2n+1))/6) ∼(1/(2n))−(2/n) →0 (n→∞) lim_(n→+∞) (1/n^2 ) Σ_(k=1) ^n (√(k(n−k)))=lim_(n→+∞) (1/n)Σ_(k=1) ^n (√((k(n−k))/n^2 )) =lim_(n→+∞) (1/n)Σ_(k=1) ^n (√((k/n)−((k/n))^2 )) =∫_0 ^1 (√(x−x^2 ))dx =∫_0 ^1 (√x)×(√(1−x))dx =_(x =sin^2 θ) ∫_0 ^(π/2) sinθ ×cosθ (2sinθ cosθ)dθ =2 ∫_0 ^(π/2) (sinθ cosθ)^2 dθ =2 ∫_0 ^(π/2) ((1/2)sin(2θ))^(2 ) dθ =(1/2) ∫_0 ^(π/2) ((1−cos(4θ))/2) dθ =(1/4)×(π/2) −(1/(16))[sin(4θ)]_0 ^(π/2) =(π/8) ⇒ lim_(n→+∞) ln(A_n ) =(π/8) ⇒lim_(n→+∞) A_n =e^(π/8)](https://www.tinkutara.com/question/Q112252.png)
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{1}+\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{ln}\left(\mathrm{A}_{\mathrm{n}} \right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\mathrm{1}−\mathrm{x}\:+\mathrm{x}^{\mathrm{2}} −…\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−…\:\Rightarrow\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\leqslant\mathrm{x}\:\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }−\frac{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}{\mathrm{n}^{\mathrm{4}} }\:\leqslant\mathrm{ln}\left(\mathrm{1}+\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }\right)\leqslant\frac{\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}}{\mathrm{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\:\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)\leqslant\mathrm{ln}\left(\mathrm{A}_{\mathrm{n}} \right)\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}\:} \left(\mathrm{nk}−\mathrm{k}^{\mathrm{2}} \right)\:=\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }×\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\:\sim\frac{\mathrm{1}}{\mathrm{2n}}−\frac{\mathrm{2}}{\mathrm{n}}\:\rightarrow\mathrm{0}\:\:\left(\mathrm{n}\rightarrow\infty\right) \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\sqrt{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\frac{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)}{\mathrm{n}^{\mathrm{2}} }} \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\sqrt{\frac{\mathrm{k}}{\mathrm{n}}−\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}}×\sqrt{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=_{\mathrm{x}\:=\mathrm{sin}^{\mathrm{2}} \theta} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}\theta\:×\mathrm{cos}\theta\:\left(\mathrm{2sin}\theta\:\mathrm{cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{sin}\theta\:\mathrm{cos}\theta\right)^{\mathrm{2}} \:\mathrm{d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}\:} \mathrm{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}\:\mathrm{d}\theta\:=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{16}}\left[\mathrm{sin}\left(\mathrm{4}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{A}_{\mathrm{n}} \right)\:=\frac{\pi}{\mathrm{8}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\frac{\pi}{\mathrm{8}}} \\ $$$$ \\ $$
