Menu Close

calculate-lim-n-n-1-1-n-n-en-

Tinku Tara 0 Comments
Pin




Question Number 63215 by mathmax by abdo last updated on 30/Jun/19
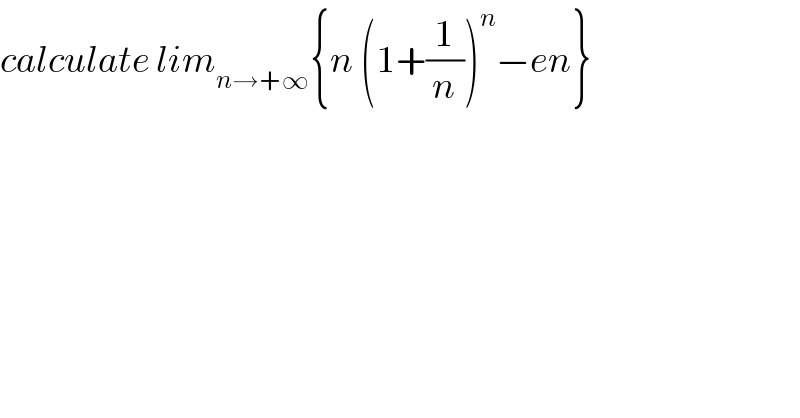
calculate lim_(n→+∞) {n (1+(1/n))^n −en}
$${calculate}\:{lim}_{{n}\rightarrow+\infty} \left\{{n}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} −{en}\right\} \\ $$
Commented by mathmax by abdo last updated on 01/Jul/19
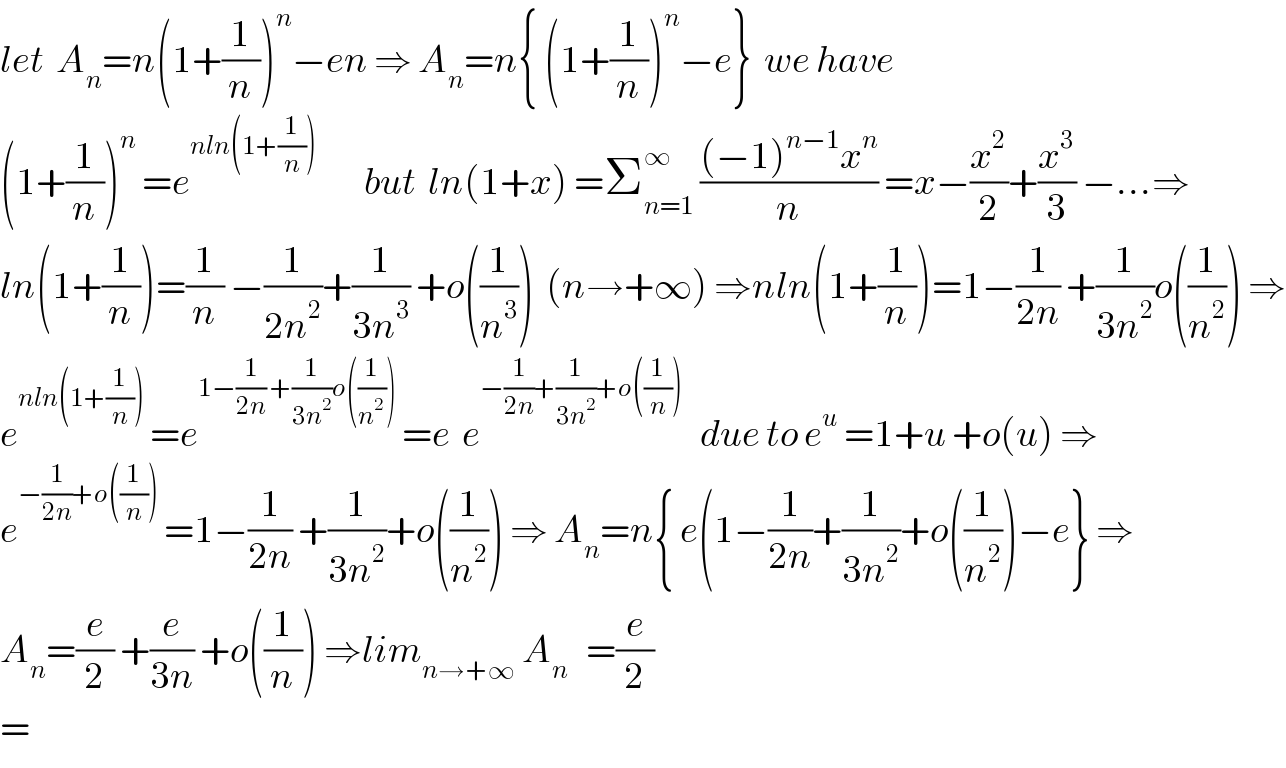
let A_n =n(1+(1/n))^n −en ⇒ A_n =n{ (1+(1/n))^n −e} we have (1+(1/n))^n =e^(nln(1+(1/n))) but ln(1+x) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n) =x−(x^2 /2)+(x^3 /3) −...⇒ ln(1+(1/n))=(1/n) −(1/(2n^2 ))+(1/(3n^3 )) +o((1/n^3 )) (n→+∞) ⇒nln(1+(1/n))=1−(1/(2n)) +(1/(3n^2 ))o((1/n^2 )) ⇒ e^(nln(1+(1/n))) =e^(1−(1/(2n)) +(1/(3n^2 ))o((1/n^2 ))) =e e^(−(1/(2n))+(1/(3n^2 ))+o((1/n))) due to e^u =1+u +o(u) ⇒ e^(−(1/(2n))+o((1/n))) =1−(1/(2n)) +(1/(3n^2 ))+o((1/n^2 )) ⇒ A_n =n{ e(1−(1/(2n))+(1/(3n^2 ))+o((1/n^2 ))−e} ⇒ A_n =(e/2) +(e/(3n)) +o((1/n)) ⇒lim_(n→+∞) A_n =(e/2) =
$${let}\:\:{A}_{{n}} ={n}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} −{en}\:\Rightarrow\:{A}_{{n}} ={n}\left\{\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} −{e}\right\}\:\:{we}\:{have} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:={e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:\:\:\:\:\:\:\:{but}\:\:{ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}\:={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−…\Rightarrow \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{3}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\:\:\left({n}\rightarrow+\infty\right)\:\Rightarrow{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:={e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)} \:={e}\:\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}}\right)} \:\:\:{due}\:{to}\:{e}^{{u}} \:=\mathrm{1}+{u}\:+{o}\left({u}\right)\:\Rightarrow \\ $$$${e}^{−\frac{\mathrm{1}}{\mathrm{2}{n}}+{o}\left(\frac{\mathrm{1}}{{n}}\right)} \:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow\:{A}_{{n}} ={n}\left\{\:{e}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−{e}\right\}\:\Rightarrow\right. \\ $$$${A}_{{n}} =\frac{{e}}{\mathrm{2}}\:+\frac{{e}}{\mathrm{3}{n}}\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \:\:\:=\frac{{e}}{\mathrm{2}} \\ $$$$= \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *