Question Number 34217 by abdo imad last updated on 02/May/18
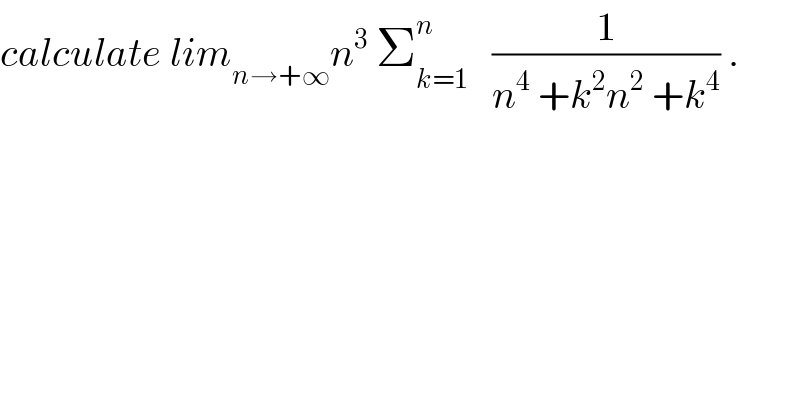
$${calculate}\:{lim}_{{n}\rightarrow+\infty} {n}^{\mathrm{3}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} \:+{k}^{\mathrm{2}} {n}^{\mathrm{2}} \:+{k}^{\mathrm{4}} }\:. \\ $$
Commented by math khazana by abdo last updated on 04/May/18
![let put S_n = n^3 Σ_(k=1) ^n (1/(n^4 +k^2 n^2 +k^4 )) S_n = (1/n) Σ_(k=1) ^(n ) (1/(1+(k^2 /n^2 ) + (k^4 /n^4 ))) so S_n is a Rieman sum and lim_(n→+∞) S_n = ∫_0 ^1 (dx/(1+x^2 +x^4 )) x^4 +x^2 +1 = (x^2 +1)^2 −x^2 =(x^2 +1−x)(x^2 +1+x) let decompose F(x)= (1/((x^2 +x+1)(x^2 −x+1))) F(x) = ((ax+b)/(x^2 +x+1)) +((cx+d)/(x^2 −x+1)) F(−x) =F(x)⇒ ((−ax+b)/(x^2 −x+1)) +((−cx +d)/(x^2 +x+1)) =F(x) ⇒ c=−a and b=d ⇒ F(x) = ((ax+b)/(x^2 +x+1)) +((−ax +b)/(x^2 −x +1)) F(0) =1 = 2b ⇒ b=(1/2) ⇒ F(x)= (1/2)( ((2ax+1)/(x^2 +x+1)) +((−2ax +1)/(x^2 −x+1))) F(1) =(1/3) = (1/2)( ((2a+1)/3) +((−2a+1)/1))⇒ 1=(1/2)( 2a +1 −6a+3)=(1/2)(−4a+4)= −2a+2 ⇒ −2a=−1 ⇒ a =(1/2) ⇒ F(x) =(1/2)( ((x+1)/(x^2 +x+1)) −((x−1)/(x^2 −x +1))) ∫_0 ^1 (dx/(x^4 +x^2 +1)) =(1/4)∫_0 ^1 ((2x+2)/(x^2 +x +1))dx −(1/4)∫_0 ^1 ((2x−2)/(x^2 +x+1))dx ∫_0 ^1 ((2x+2)/(x^2 +x+1))dx =∫_0 ^1 ((2x+1)/(x^2 +x+1))dx +∫_0 ^1 (dx/(x^2 +x+1)) =[ln(x^2 +x+1)]_0 ^1 + ∫_0 ^1 (dx/((x+(1/2))^2 +(3/4))) (x+(1/2)=((√3)/2)u =ln(3) + ∫_(1/( (√3))) ^(√3) (1/((3/4)( 1+u^2 ))) ((√3)/2)du =ln(3) +(4/3) ((√3)/2) ∫_(1/( (√3))) ^(√3) (du/(1+u^2 )) =ln(3) +((2(√3))/3) (arctan((√3)) −arctan((1/( (√3))))) ....](https://www.tinkutara.com/question/Q34337.png)
$${let}\:{put}\:{S}_{{n}} \:=\:{n}^{\mathrm{3}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} \:+{k}^{\mathrm{2}} {n}^{\mathrm{2}} \:+{k}^{\mathrm{4}} } \\ $$$${S}_{{n}} =\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}\:} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:+\:\frac{{k}^{\mathrm{4}} }{{n}^{\mathrm{4}} }}\:\:{so}\:{S}_{{n}} \:{is}\:{a}\:{Rieman}\:{sum} \\ $$$${and}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} } \\ $$$${x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}\:=\:\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:−{x}^{\mathrm{2}} =\left({x}^{\mathrm{2}} \:+\mathrm{1}−{x}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}+{x}\right) \\ $$$${let}\:{decompose}\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)\:=\:\frac{{ax}+{b}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${F}\left(−{x}\right)\:={F}\left({x}\right)\Rightarrow\:\frac{−{ax}+{b}}{{x}^{\mathrm{2}} \:−{x}+\mathrm{1}}\:+\frac{−{cx}\:+{d}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:={F}\left({x}\right)\:\Rightarrow \\ $$$${c}=−{a}\:\:{and}\:\:{b}={d}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{{ax}+{b}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\frac{−{ax}\:+{b}}{{x}^{\mathrm{2}} \:−{x}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\:\mathrm{2}{b}\:\Rightarrow\:{b}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:\frac{\mathrm{2}{ax}+\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:+\frac{−\mathrm{2}{ax}\:+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right) \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:\frac{\mathrm{2}{a}+\mathrm{1}}{\mathrm{3}}\:+\frac{−\mathrm{2}{a}+\mathrm{1}}{\mathrm{1}}\right)\Rightarrow \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:\mathrm{2}{a}\:+\mathrm{1}\:−\mathrm{6}{a}+\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{4}{a}+\mathrm{4}\right)=\:−\mathrm{2}{a}+\mathrm{2}\:\Rightarrow \\ $$$$−\mathrm{2}{a}=−\mathrm{1}\:\Rightarrow\:{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:−\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} \:−{x}\:+\mathrm{1}}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{x}+\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}\:+\mathrm{1}}{dx}\:−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}−\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{x}+\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$=\left[{ln}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:+\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}\right. \\ $$$$={ln}\left(\mathrm{3}\right)\:\:+\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\:\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$={ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\: \\ $$$$={ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\left({arctan}\left(\sqrt{\mathrm{3}}\right)\:−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)\:…. \\ $$
