Question Number 157171 by mathocean1 last updated on 20/Oct/21
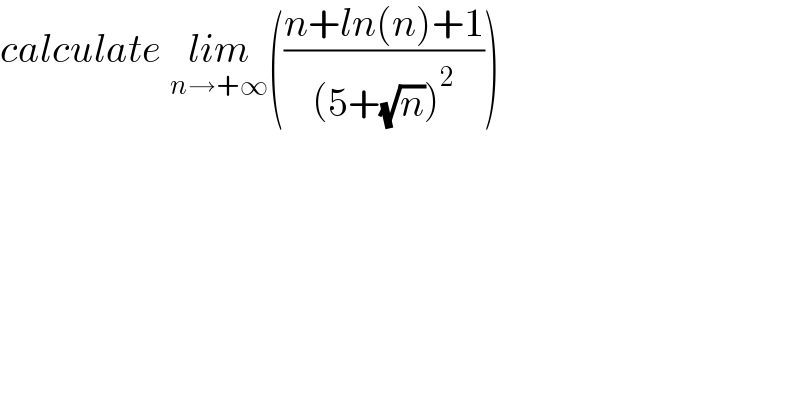
$${calculate}\:\underset{{n}\rightarrow+\infty} {{lim}}\left(\frac{{n}+{ln}\left({n}\right)+\mathrm{1}}{\left(\mathrm{5}+\sqrt{{n}}\right)^{\mathrm{2}} }\right) \\ $$
Answered by puissant last updated on 20/Oct/21
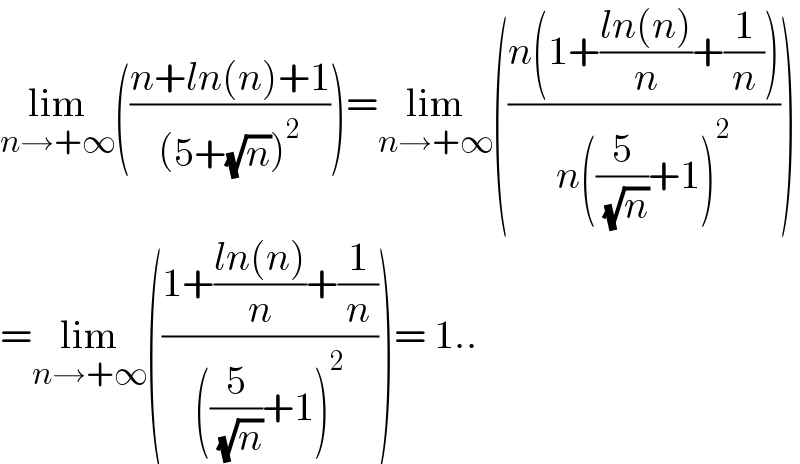
$$\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{n}+{ln}\left({n}\right)+\mathrm{1}}{\left(\mathrm{5}+\sqrt{{n}}\right)^{\mathrm{2}} }\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{n}\left(\mathrm{1}+\frac{{ln}\left({n}\right)}{{n}}+\frac{\mathrm{1}}{{n}}\right)}{{n}\left(\frac{\mathrm{5}}{\:\sqrt{{n}}}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}+\frac{{ln}\left({n}\right)}{{n}}+\frac{\mathrm{1}}{{n}}}{\left(\frac{\mathrm{5}}{\:\sqrt{{n}}}+\mathrm{1}\right)^{\mathrm{2}} }\right)=\:\mathrm{1}.. \\ $$
Commented by mathocean1 last updated on 22/Oct/21
$${thanks}\:{le}\:{puissant}. \\ $$
