calculate-lim-n-n-n-n-n-

Question Number 62659 by mathmax by abdo last updated on 24/Jun/19

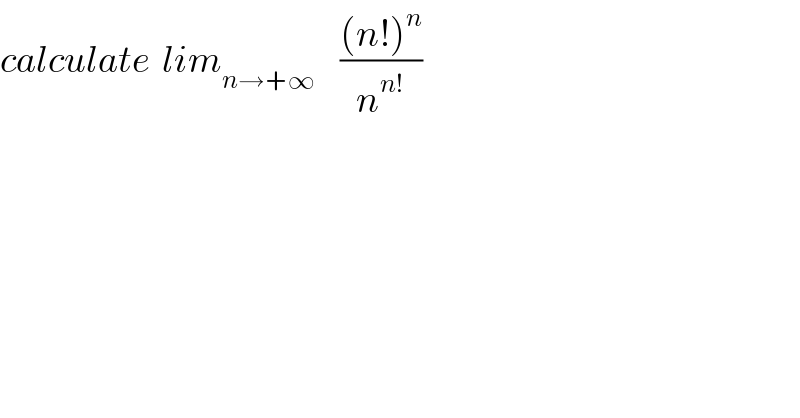
$${calculate}\:\:{lim}_{{n}\rightarrow+\infty} \:\:\:\:\frac{\left({n}!\right)^{{n}} }{{n}^{{n}!} } \\ $$

Commented by abdo mathsup 649 cc last updated on 24/Jun/19

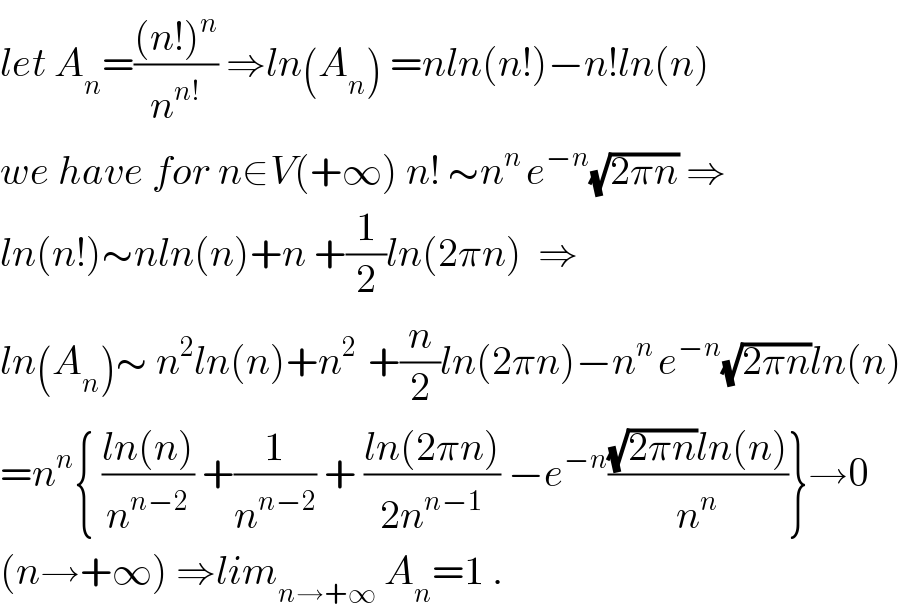
let A_n =(((n!)^n )/n^(n!) ) ⇒ln(A_n ) =nln(n!)−n!ln(n) we have for n∈V(+∞) n! ∼n^(n ) e^(−n) (√(2πn)) ⇒ ln(n!)∼nln(n)+n +(1/2)ln(2πn) ⇒ ln(A_n )∼ n^2 ln(n)+n^(2 ) +(n/2)ln(2πn)−n^(n ) e^(−n) (√(2πn))ln(n) =n^n { ((ln(n))/n^(n−2) ) +(1/n^(n−2) ) + ((ln(2πn))/(2n^(n−1) )) −e^(−n) (((√(2πn))ln(n))/n^n )}→0 (n→+∞) ⇒lim_(n→+∞) A_n =1 .

$${let}\:{A}_{{n}} =\frac{\left({n}!\right)^{{n}} }{{n}^{{n}!} }\:\Rightarrow{ln}\left({A}_{{n}} \right)\:={nln}\left({n}!\right)−{n}!{ln}\left({n}\right)\: \\ $$$${we}\:{have}\:{for}\:{n}\in{V}\left(+\infty\right)\:{n}!\:\sim{n}^{{n}\:} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:\Rightarrow \\ $$$${ln}\left({n}!\right)\sim{nln}\left({n}\right)+{n}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi{n}\right)\:\:\Rightarrow \\ $$$${ln}\left({A}_{{n}} \right)\sim\:{n}^{\mathrm{2}} {ln}\left({n}\right)+{n}^{\mathrm{2}\:} \:+\frac{{n}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi{n}\right)−{n}^{{n}\:} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}{ln}\left({n}\right) \\ $$$$={n}^{{n}} \left\{\:\frac{{ln}\left({n}\right)}{{n}^{{n}−\mathrm{2}} }\:+\frac{\mathrm{1}}{{n}^{{n}−\mathrm{2}} }\:+\:\frac{{ln}\left(\mathrm{2}\pi{n}\right)}{\mathrm{2}{n}^{{n}−\mathrm{1}} }\:−{e}^{−{n}} \frac{\sqrt{\mathrm{2}\pi{n}}{ln}\left({n}\right)}{{n}^{{n}} }\right\}\rightarrow\mathrm{0} \\ $$$$\left({n}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\mathrm{1}\:. \\ $$

Commented by abdo mathsup 649 cc last updated on 24/Jun/19

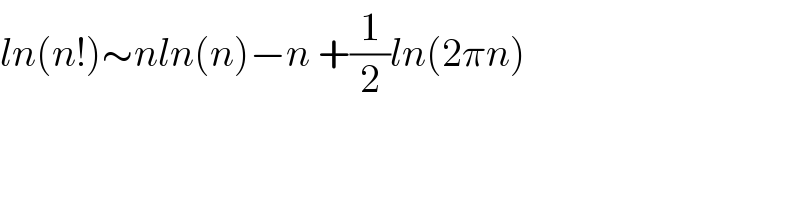
$${ln}\left({n}!\right)\sim{nln}\left({n}\right)−{n}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi{n}\right) \\ $$

Commented by MJS last updated on 24/Jun/19

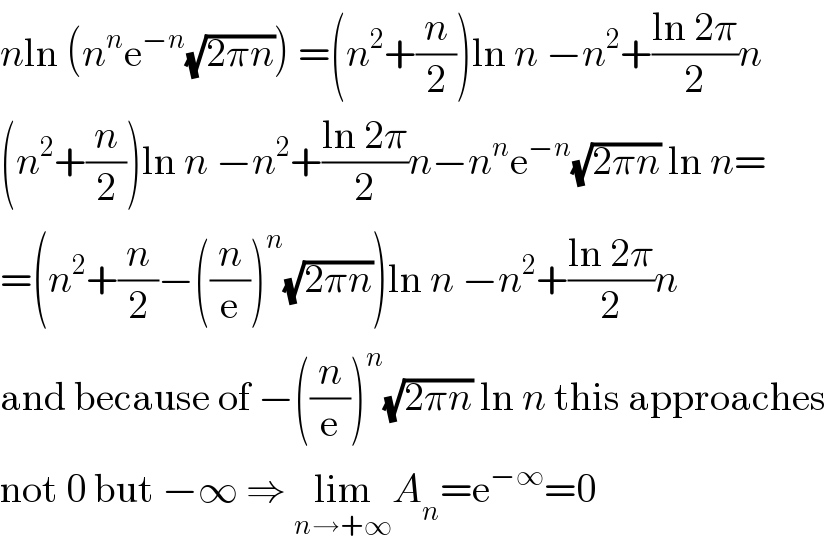
nln (n^n e^(−n) (√(2πn))) =(n^2 +(n/2))ln n −n^2 +((ln 2π)/2)n (n^2 +(n/2))ln n −n^2 +((ln 2π)/2)n−n^n e^(−n) (√(2πn)) ln n= =(n^2 +(n/2)−((n/e))^n (√(2πn)))ln n −n^2 +((ln 2π)/2)n and because of −((n/e))^n (√(2πn)) ln n this approaches not 0 but −∞ ⇒ lim_(n→+∞) A_n =e^(−∞) =0

$${n}\mathrm{ln}\:\left({n}^{{n}} \mathrm{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\right)\:=\left({n}^{\mathrm{2}} +\frac{{n}}{\mathrm{2}}\right)\mathrm{ln}\:{n}\:−{n}^{\mathrm{2}} +\frac{\mathrm{ln}\:\mathrm{2}\pi}{\mathrm{2}}{n} \\ $$$$\left({n}^{\mathrm{2}} +\frac{{n}}{\mathrm{2}}\right)\mathrm{ln}\:{n}\:−{n}^{\mathrm{2}} +\frac{\mathrm{ln}\:\mathrm{2}\pi}{\mathrm{2}}{n}−{n}^{{n}} \mathrm{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:\mathrm{ln}\:{n}= \\ $$$$=\left({n}^{\mathrm{2}} +\frac{{n}}{\mathrm{2}}−\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}\right)\mathrm{ln}\:{n}\:−{n}^{\mathrm{2}} +\frac{\mathrm{ln}\:\mathrm{2}\pi}{\mathrm{2}}{n} \\ $$$$\mathrm{and}\:\mathrm{because}\:\mathrm{of}\:−\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}\:\mathrm{ln}\:{n}\:\mathrm{this}\:\mathrm{approaches} \\ $$$$\mathrm{not}\:\mathrm{0}\:\mathrm{but}\:−\infty\:\Rightarrow\:\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{A}_{{n}} =\mathrm{e}^{−\infty} =\mathrm{0} \\ $$

Answered by MJS last updated on 24/Jun/19

(((n!)^n )/n^(n!) )=f(n) f(1)=(1/1)=1 f(2)=(4/4)=1 f(3)=((216)/(729))=(8/(27)) f(4)=((331776)/(281474976710656))=((81)/(68719476736)) ... f(∞)=0

$$\frac{\left({n}!\right)^{{n}} }{{n}^{{n}!} }={f}\left({n}\right) \\ $$$${f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$${f}\left(\mathrm{2}\right)=\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)=\frac{\mathrm{216}}{\mathrm{729}}=\frac{\mathrm{8}}{\mathrm{27}} \\ $$$${f}\left(\mathrm{4}\right)=\frac{\mathrm{331776}}{\mathrm{281474976710656}}=\frac{\mathrm{81}}{\mathrm{68719476736}} \\ $$$$… \\ $$$${f}\left(\infty\right)=\mathrm{0} \\ $$

Facebook Tweet Pin

calculate-lim-n-n-n-n-n-

Leave a Reply Cancel reply