Question Number 57405 by Abdo msup. last updated on 03/Apr/19
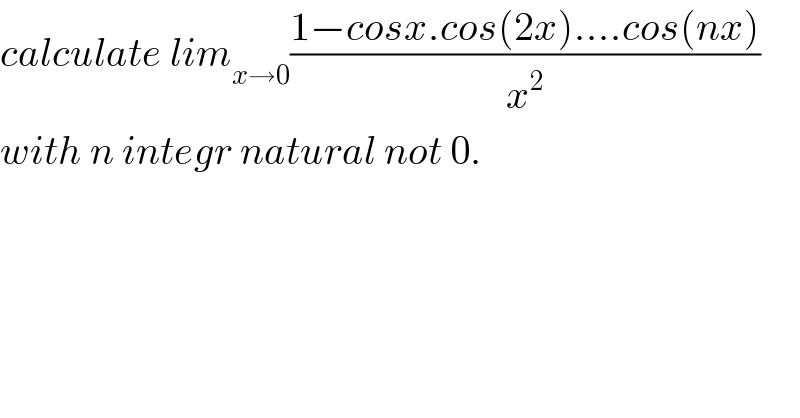
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cosx}.{cos}\left(\mathrm{2}{x}\right)….{cos}\left({nx}\right)}{{x}^{\mathrm{2}} } \\ $$$${with}\:{n}\:{integr}\:{natural}\:{not}\:\mathrm{0}. \\ $$
Answered by Smail last updated on 05/Apr/19
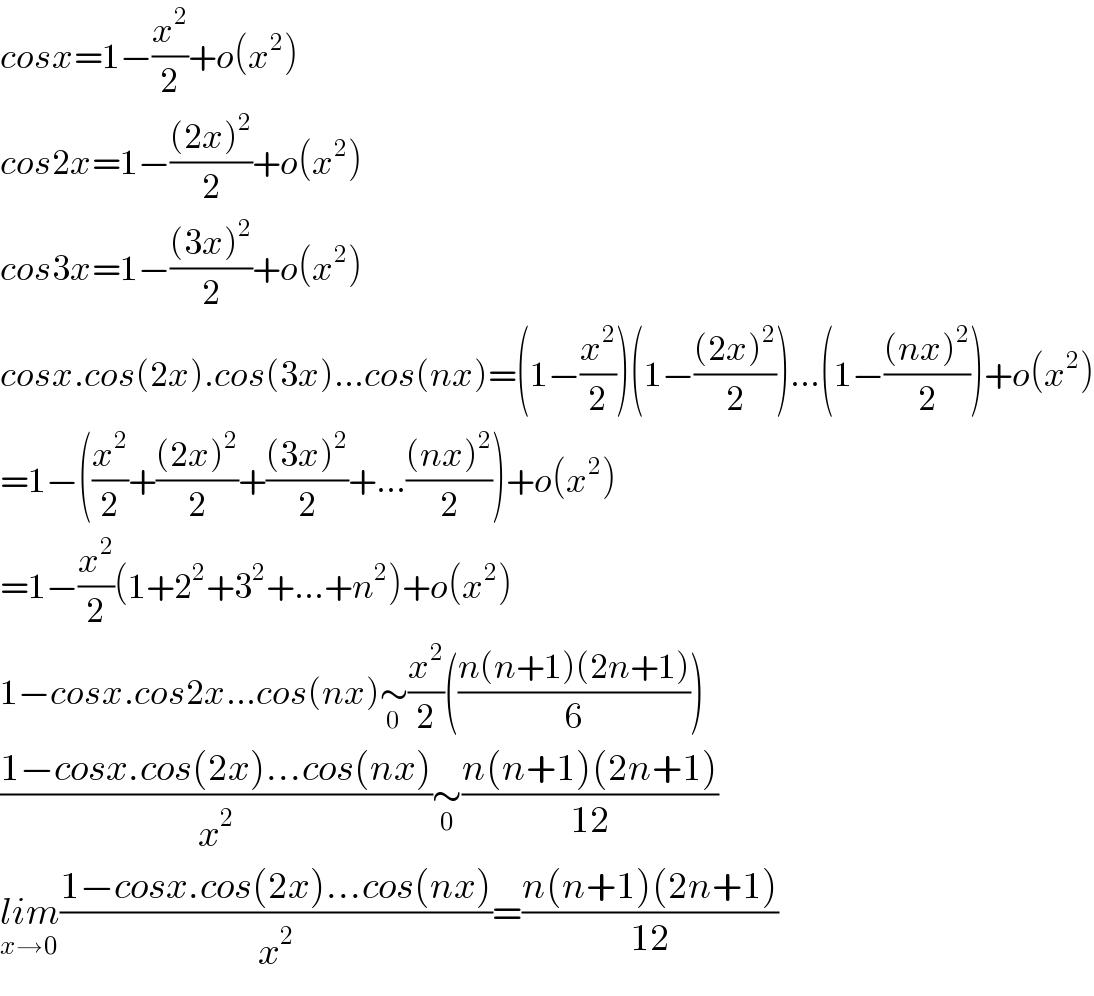
$${cosx}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${cos}\mathrm{2}{x}=\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${cos}\mathrm{3}{x}=\mathrm{1}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$${cosx}.{cos}\left(\mathrm{2}{x}\right).{cos}\left(\mathrm{3}{x}\right)…{cos}\left({nx}\right)=\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\right)…\left(\mathrm{1}−\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}−\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+…\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +…+{n}^{\mathrm{2}} \right)+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$\mathrm{1}−{cosx}.{cos}\mathrm{2}{x}…{cos}\left({nx}\right)\underset{\mathrm{0}} {\sim}\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right) \\ $$$$\frac{\mathrm{1}−{cosx}.{cos}\left(\mathrm{2}{x}\right)…{cos}\left({nx}\right)}{{x}^{\mathrm{2}} }\underset{\mathrm{0}} {\sim}\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{cosx}.{cos}\left(\mathrm{2}{x}\right)…{cos}\left({nx}\right)}{{x}^{\mathrm{2}} }=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}} \\ $$
