Question Number 168055 by qaz last updated on 01/Apr/22

$$\mathrm{Calculate}\:::\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }} }{\mathrm{x}}=? \\ $$
Answered by LEKOUMA last updated on 03/Apr/22

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\left(\left(\mathrm{1}+{x}\right)−\mathrm{1}\right)\frac{\mathrm{1}}{{x}^{\mathrm{3}} }} }{{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} }{{x}}=+\infty \\ $$
Answered by Mathspace last updated on 04/Apr/22
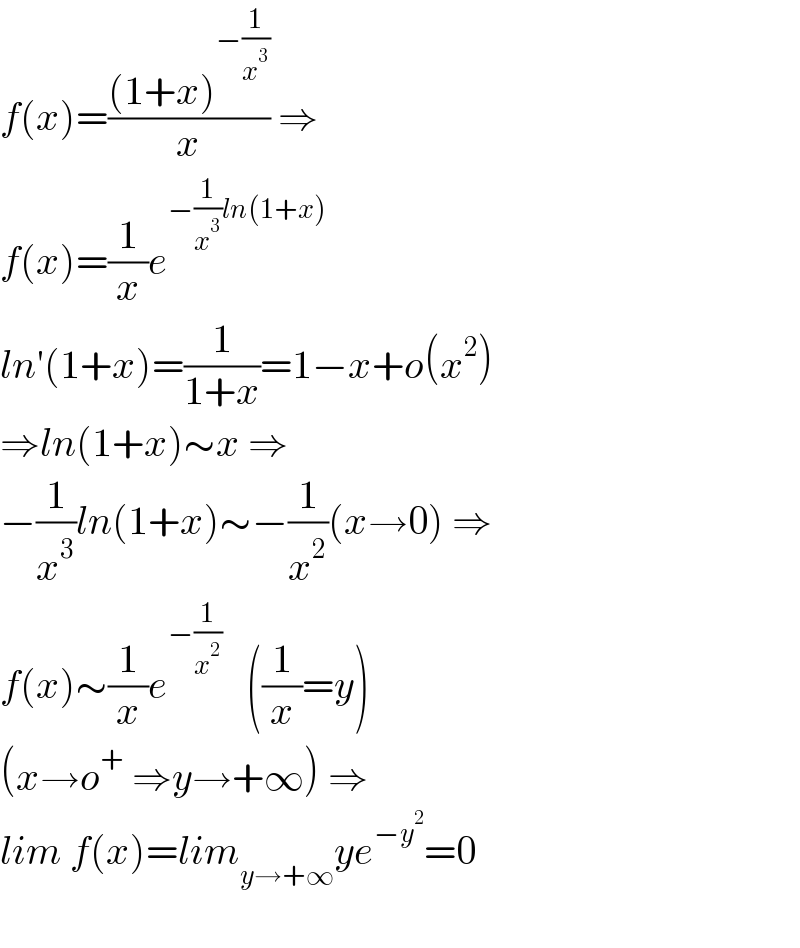
$${f}\left({x}\right)=\frac{\left(\mathrm{1}+{x}\right)^{−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }} }{{x}}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}}{e}^{−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }{ln}\left(\mathrm{1}+{x}\right)} \:\:\: \\ $$$${ln}'\left(\mathrm{1}+{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}}=\mathrm{1}−{x}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\sim{x}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }{ln}\left(\mathrm{1}+{x}\right)\sim−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}}{{x}}{e}^{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\:\:\left(\frac{\mathrm{1}}{{x}}={y}\right) \\ $$$$\left({x}\rightarrow{o}^{+} \:\Rightarrow{y}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}\:{f}\left({x}\right)={lim}_{{y}\rightarrow+\infty} {ye}^{−{y}^{\mathrm{2}} } =\mathrm{0} \\ $$$$ \\ $$
