Question Number 31675 by gunawan last updated on 12/Mar/18
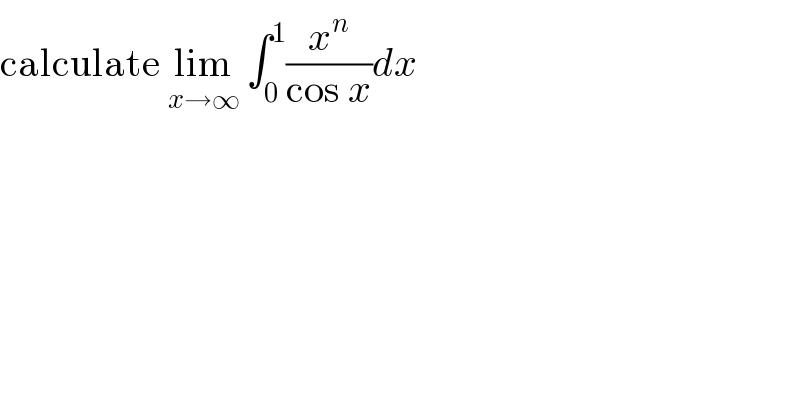
$$\mathrm{calculate}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{\mathrm{cos}\:{x}}{dx} \\ $$
Commented by abdo imad last updated on 12/Mar/18
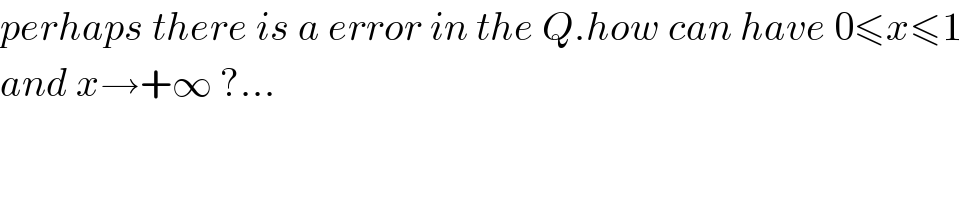
$${perhaps}\:{there}\:{is}\:{a}\:{error}\:{in}\:{the}\:{Q}.{how}\:{can}\:{have}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1} \\ $$$${and}\:{x}\rightarrow+\infty\:?… \\ $$
Commented by gunawan last updated on 12/Mar/18

$$\mathrm{I}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{Sir},\:\mathrm{in}\:\mathrm{written}\:\mathrm{like}\:\mathrm{that} \\ $$
Commented by Joel578 last updated on 13/Mar/18
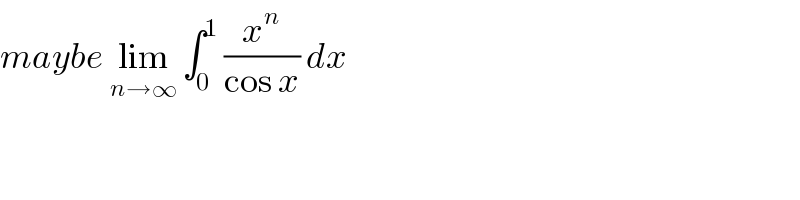
$${maybe}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\mathrm{cos}\:{x}}\:{dx} \\ $$
Commented by abdo imad last updated on 13/Mar/18
![let use the ch. x^n =t ⇔ x=t^(1/n) and A_n =∫_0 ^1 (x^n /(cosx)) dx= ∫_0 ^1 (t/(cos(t^(1/n) ))) (1/n) t^((1/n)−1) dt =(1/n) ∫_0 ^1 (t^(1/n) /(cos(t^(1/n) )))dt =(1/n) ∫_R (t^(1/n) /(cos(t^(1/n) ))) χ_([0,1]) (t)dt the sequence of functions f_n (t)= (t^(1/n) /(cos(t^(1/n) ))) χ_([0,1]) (t) c.s.to χ_([0,1]) (t) ⇒ lim_(n→∞) A_n =lim_(n→∞) (1/n) ∫_R χ_([0,1]) (t)dt=0](https://www.tinkutara.com/question/Q31752.png)
$${let}\:{use}\:{the}\:{ch}.\:{x}^{{n}} ={t}\:\Leftrightarrow\:{x}={t}^{\frac{\mathrm{1}}{{n}}} \:\:{and} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{n}} }{{cosx}}\:{dx}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}}{{cos}\left({t}^{\frac{\mathrm{1}}{{n}}} \right)}\:\frac{\mathrm{1}}{{n}}\:{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{t}^{\frac{\mathrm{1}}{{n}}} }{{cos}\left({t}^{\frac{\mathrm{1}}{{n}}} \right)}{dt}\:=\frac{\mathrm{1}}{{n}}\:\int_{{R}} \:\:\frac{{t}^{\frac{\mathrm{1}}{{n}}} }{{cos}\left({t}^{\frac{\mathrm{1}}{{n}}} \right)}\:\chi_{\left[\mathrm{0},\mathrm{1}\right]} \left({t}\right){dt}\:{the} \\ $$$${sequence}\:{of}\:{functions}\:\:{f}_{{n}} \left({t}\right)=\:\frac{{t}^{\frac{\mathrm{1}}{{n}}} }{{cos}\left({t}^{\frac{\mathrm{1}}{{n}}} \right)}\:\chi_{\left[\mathrm{0},\mathrm{1}\right]} \left({t}\right)\:{c}.{s}.{to} \\ $$$$\chi_{\left[\mathrm{0},\mathrm{1}\right]} \left({t}\right)\:\Rightarrow\:{lim}_{{n}\rightarrow\infty} \:{A}_{{n}} ={lim}_{{n}\rightarrow\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{{R}} \:\chi_{\left[\mathrm{0},\mathrm{1}\right]} \left({t}\right){dt}=\mathrm{0} \\ $$
