Question Number 42788 by maxmathsup by imad last updated on 02/Sep/18
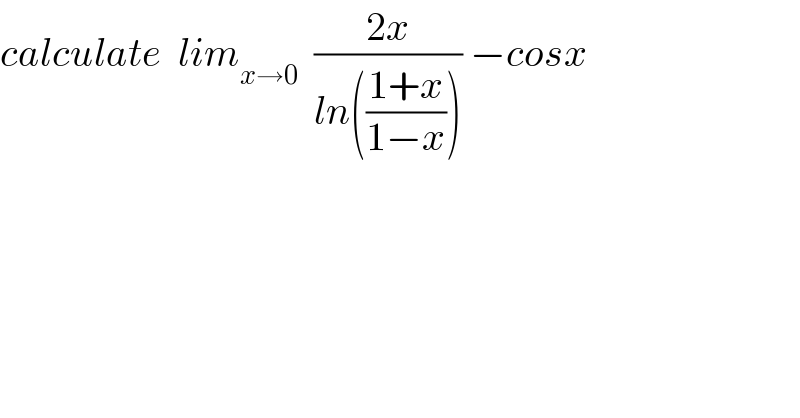
$${calculate}\:\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{2}{x}}{{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)}\:−{cosx} \\ $$
Commented by maxmathsup by imad last updated on 30/Sep/18
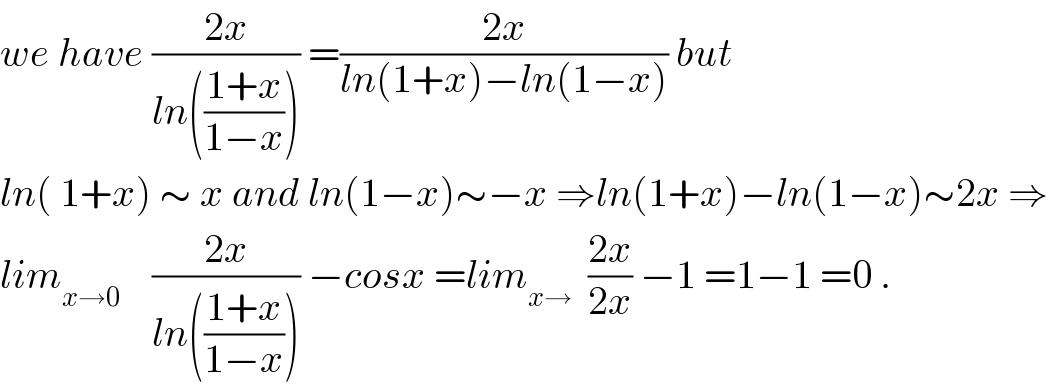
$${we}\:{have}\:\frac{\mathrm{2}{x}}{{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)}\:=\frac{\mathrm{2}{x}}{{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)}\:{but} \\ $$$${ln}\left(\:\mathrm{1}+{x}\right)\:\sim\:{x}\:{and}\:{ln}\left(\mathrm{1}−{x}\right)\sim−{x}\:\Rightarrow{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\sim\mathrm{2}{x}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\mathrm{2}{x}}{{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)}\:−{cosx}\:={lim}_{{x}\rightarrow} \:\:\frac{\mathrm{2}{x}}{\mathrm{2}{x}}\:−\mathrm{1}\:=\mathrm{1}−\mathrm{1}\:=\mathrm{0}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
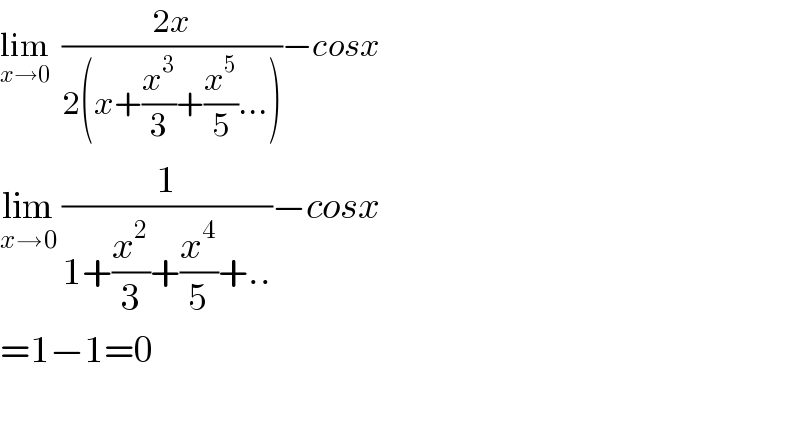
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{2}{x}}{\mathrm{2}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}…\right)}−{cosx} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{5}}+..}−{cosx} \\ $$$$=\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$
