Question Number 56332 by maxmathsup by imad last updated on 14/Mar/19
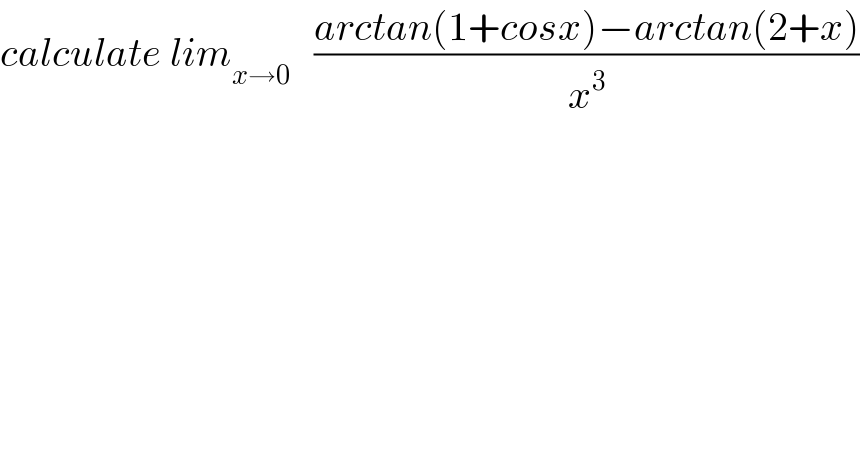
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{arctan}\left(\mathrm{1}+{cosx}\right)−{arctan}\left(\mathrm{2}+{x}\right)}{{x}^{\mathrm{3}} } \\ $$
Answered by kaivan.ahmadi last updated on 07/Apr/19
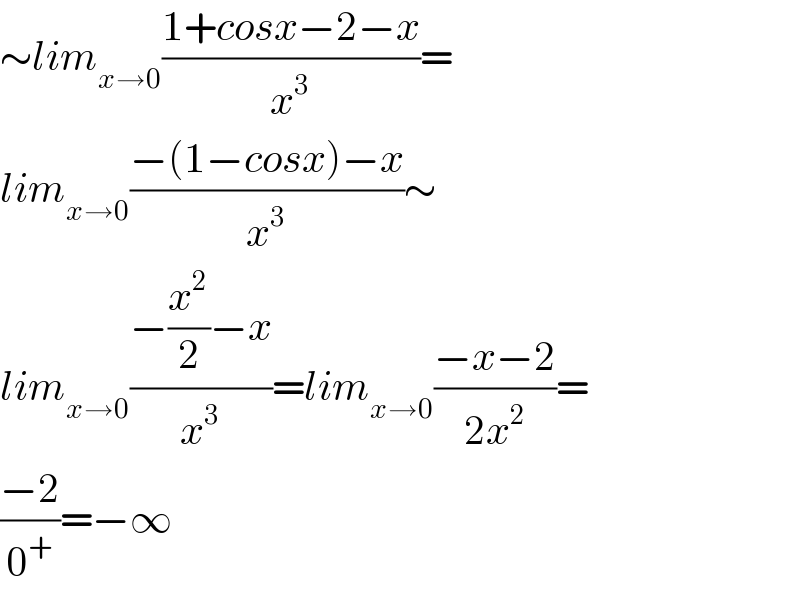
$$\sim{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}+{cosx}−\mathrm{2}−{x}}{{x}^{\mathrm{3}} }= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{−\left(\mathrm{1}−{cosx}\right)−{x}}{{x}^{\mathrm{3}} }\sim \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}}{{x}^{\mathrm{3}} }={lim}_{{x}\rightarrow\mathrm{0}} \frac{−{x}−\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} }= \\ $$$$\frac{−\mathrm{2}}{\mathrm{0}^{+} }=−\infty \\ $$
Commented by maxmathsup by imad last updated on 07/Apr/19
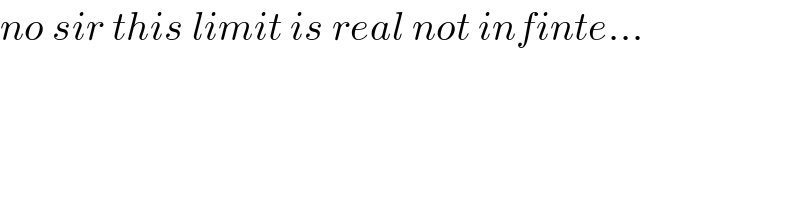
$${no}\:{sir}\:{this}\:{limit}\:{is}\:{real}\:{not}\:{infinte}… \\ $$
