Question Number 62200 by maxmathsup by imad last updated on 17/Jun/19
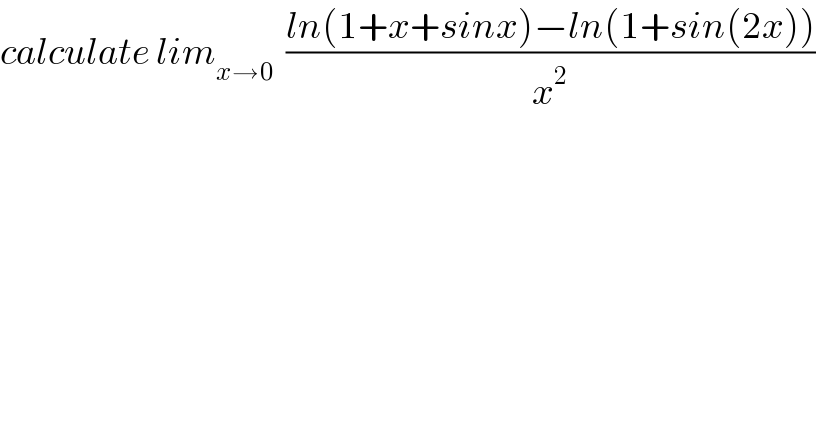
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{x}+{sinx}\right)−{ln}\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)}{{x}^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 18/Jun/19
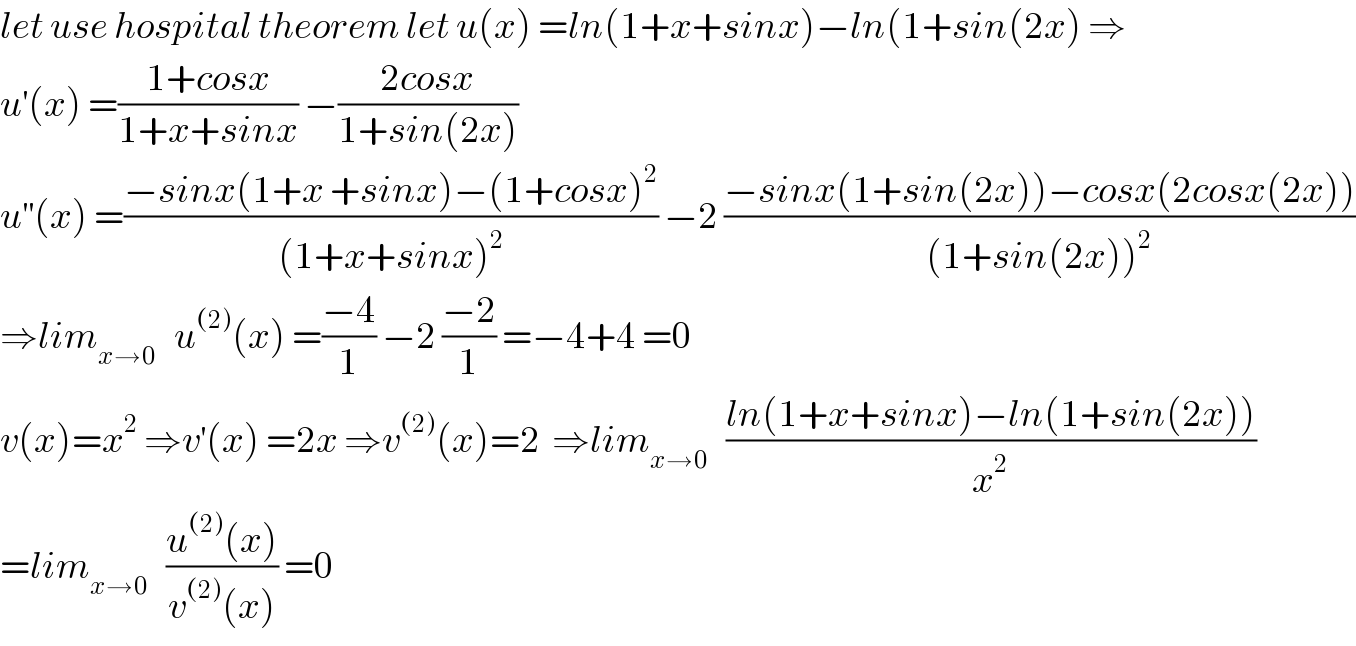
$${let}\:{use}\:{hospital}\:{theorem}\:{let}\:{u}\left({x}\right)\:={ln}\left(\mathrm{1}+{x}+{sinx}\right)−{ln}\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\:\Rightarrow\right. \\ $$$${u}^{'} \left({x}\right)\:=\frac{\mathrm{1}+{cosx}}{\mathrm{1}+{x}+{sinx}}\:−\frac{\mathrm{2}{cosx}}{\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)} \\ $$$${u}^{''} \left({x}\right)\:=\frac{−{sinx}\left(\mathrm{1}+{x}\:+{sinx}\right)−\left(\mathrm{1}+{cosx}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}+{sinx}\right)^{\mathrm{2}} }\:−\mathrm{2}\:\frac{−{sinx}\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)−{cosx}\left(\mathrm{2}{cosx}\left(\mathrm{2}{x}\right)\right)}{\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:{u}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\frac{−\mathrm{4}}{\mathrm{1}}\:−\mathrm{2}\:\frac{−\mathrm{2}}{\mathrm{1}}\:=−\mathrm{4}+\mathrm{4}\:=\mathrm{0} \\ $$$${v}\left({x}\right)={x}^{\mathrm{2}} \:\Rightarrow{v}^{'} \left({x}\right)\:=\mathrm{2}{x}\:\Rightarrow{v}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}\:\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}+{sinx}\right)−{ln}\left(\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)\right)}{{x}^{\mathrm{2}} } \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{u}^{\left(\mathrm{2}\right)} \left({x}\right)}{{v}^{\left(\mathrm{2}\right)} \left({x}\right)}\:=\mathrm{0}\: \\ $$
Answered by tanmay last updated on 17/Jun/19

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\frac{\mathrm{1}+{x}+{sinx}}{\mathrm{1}+{sin}\mathrm{2}{x}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+\frac{\mathrm{1}+{x}+{sinx}}{\mathrm{1}+{sin}\mathrm{2}{x}}−\mathrm{1}\right)}{\left(\frac{\mathrm{1}+{x}+{sinx}}{\mathrm{1}+{sin}\mathrm{2}{x}}−\mathrm{1}\right)}×\frac{\frac{{x}+{sinx}−{sin}\mathrm{2}{x}}{\mathrm{1}+{sin}\mathrm{2}{x}}}{{x}^{\mathrm{2}} } \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+{sin}\mathrm{2}{x}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}+{sinx}−{sin}\mathrm{2}{x}}{{x}^{\mathrm{2}} } \\ $$$$\mathrm{1}×\mathrm{1}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+{cosx}−\mathrm{2}{cos}\mathrm{2}{x}}{\mathrm{2}{x}}\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{sinx}+\mathrm{4}{sin}\mathrm{2}{x}}{\mathrm{2}}=\mathrm{0} \\ $$$$ \\ $$
