calculate-lim-x-0-ln-1-x-x-x-2-

Question Number 32991 by abdo imad last updated on 09/Apr/18

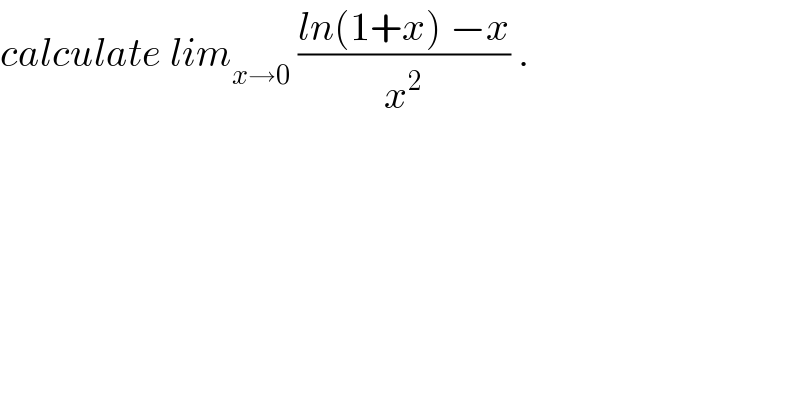
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)\:−{x}}{{x}^{\mathrm{2}} }\:. \\ $$

Commented by prof Abdo imad last updated on 09/Apr/18

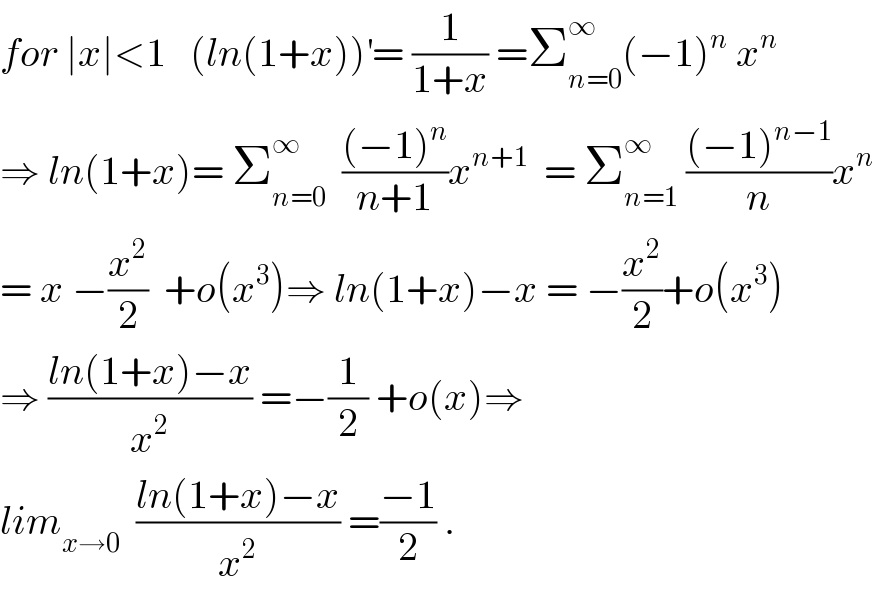
for ∣x∣<1 (ln(1+x))^′ = (1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x)= Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) = Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n = x −(x^2 /2) +o(x^3 )⇒ ln(1+x)−x = −(x^2 /2)+o(x^3 ) ⇒ ((ln(1+x)−x)/x^2 ) =−(1/2) +o(x)⇒ lim_(x→0) ((ln(1+x)−x)/x^2 ) =((−1)/2) .

$${for}\:\mid{x}\mid<\mathrm{1}\:\:\:\left({ln}\left(\mathrm{1}+{x}\right)\right)^{'} =\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \\ $$$$\Rightarrow\:{ln}\left(\mathrm{1}+{x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$$=\:{x}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:+{o}\left({x}^{\mathrm{3}} \right)\Rightarrow\:{ln}\left(\mathrm{1}+{x}\right)−{x}\:=\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\Rightarrow\:\frac{{ln}\left(\mathrm{1}+{x}\right)−{x}}{{x}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{2}}\:+{o}\left({x}\right)\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)−{x}}{{x}^{\mathrm{2}} }\:=\frac{−\mathrm{1}}{\mathrm{2}}\:. \\ $$

Answered by kyle_TW last updated on 09/Apr/18

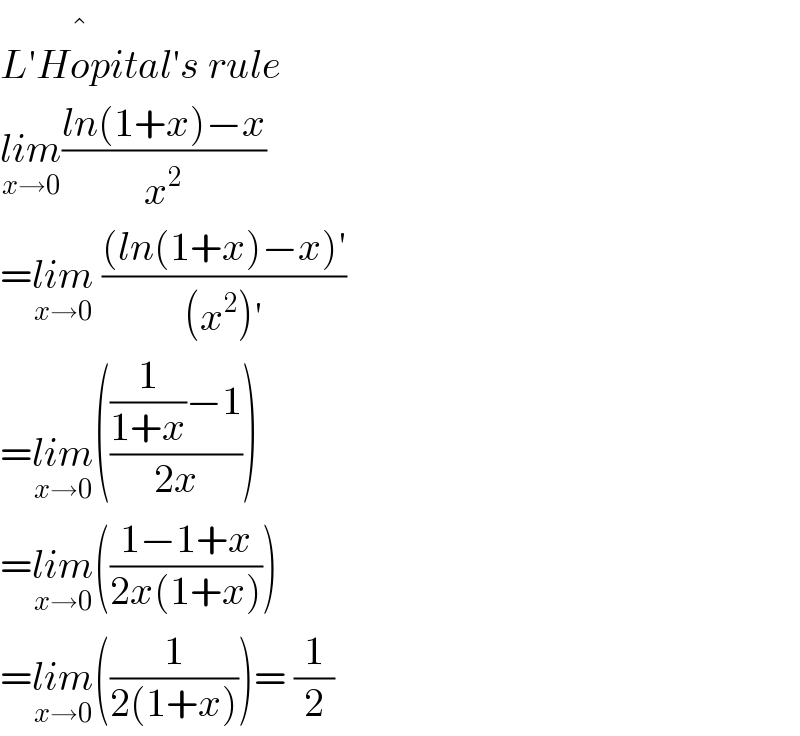
L′Ho^(�) pital′s rule lim_(x→0) ((ln(1+x)−x)/x^2 ) =lim_(x→0) (((ln(1+x)−x)′)/((x^2 )′)) =lim_(x→0) ((((1/(1+x))−1)/(2x))) =lim_(x→0) (((1−1+x)/(2x(1+x)))) =lim_(x→0) ((1/(2(1+x))))= (1/2)

$${L}'{H}\overset{} {{o}pital}'{s}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{ln}\left(\mathrm{1}+{x}\right)−{x}}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\left({ln}\left(\mathrm{1}+{x}\right)−{x}\right)'}{\left({x}^{\mathrm{2}} \right)'} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}}{\mathrm{2}{x}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{1}−\mathrm{1}+{x}}{\mathrm{2}{x}\left(\mathrm{1}+{x}\right)}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}\right)}\right)=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by MJS last updated on 09/Apr/18

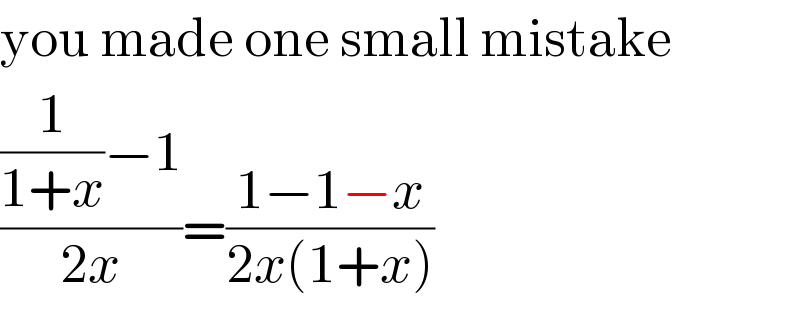
you made one small mistake (((1/(1+x))−1)/(2x))=((1−1−x)/(2x(1+x)))

$$\mathrm{you}\:\mathrm{made}\:\mathrm{one}\:\mathrm{small}\:\mathrm{mistake} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}−\mathrm{1}−{x}}{\mathrm{2}{x}\left(\mathrm{1}+{x}\right)} \\ $$

Facebook Tweet Pin

calculate-lim-x-0-ln-1-x-x-x-2-

Leave a Reply Cancel reply