Menu Close

Calculate-lim-x-0-tgx-m-sin-x-n-lim-x-0-xcos-x-x-e-x-1-ln-1-3x-2-

Tinku Tara 0 Comments
Pin




Question Number 160672 by LEKOUMA last updated on 04/Dec/21
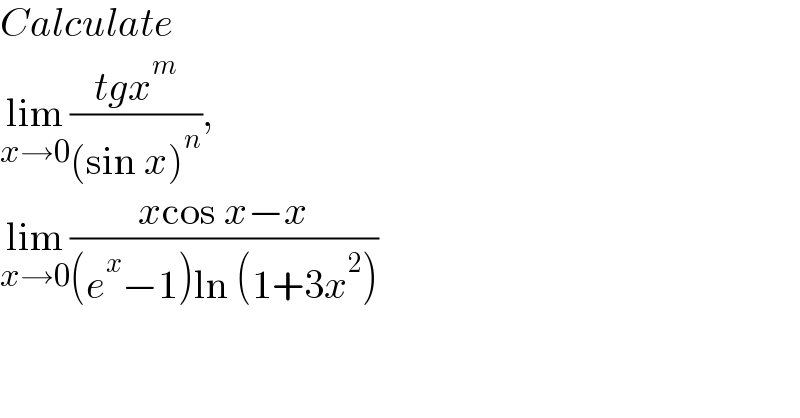
Calculate lim_(x→0) ((tgx^m )/((sin x)^n )), lim_(x→0) ((xcos x−x)/((e^x −1)ln (1+3x^2 )))
$${Calculate}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tgx}^{{m}} }{\left(\mathrm{sin}\:{x}\right)^{{n}} },\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\mathrm{cos}\:{x}−{x}}{\left({e}^{{x}} −\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} \right)} \\ $$
Commented by tounghoungko last updated on 04/Dec/21
(2) lim_(x→0) ((x cos x−x)/((e^x −1) ln (1+3x^2 ))) = lim_(x→0) ((x(cos x−1))/((e^x −1) ln (1+3x^2 ))) = lim_(x→0) (1/((((e^x −1)/x)))) × lim_(x→0) ((−2sin^2 ((1/2)x))/(ln (1+3x^2 ))) = 1× lim_(x→0) ((−(1/2)x^2 )/(ln (1+3x^2 ))) =−(1/2)× lim_(x→0) ((2x)/((((6x)/( (1+3x^2 )))))) =−(1/6) ×lim_(x→0) (1+3x^2 )= −(1/6)
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\:\mathrm{cos}\:\mathrm{x}−\mathrm{x}}{\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\:\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}}\right)}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)} \\ $$$$\:\:\:=\:\mathrm{1}×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }{\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2x}}{\left(\frac{\mathrm{6x}}{\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)}\right)}\: \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{6}}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left(\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \right)=\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by alephzero last updated on 04/Dec/21
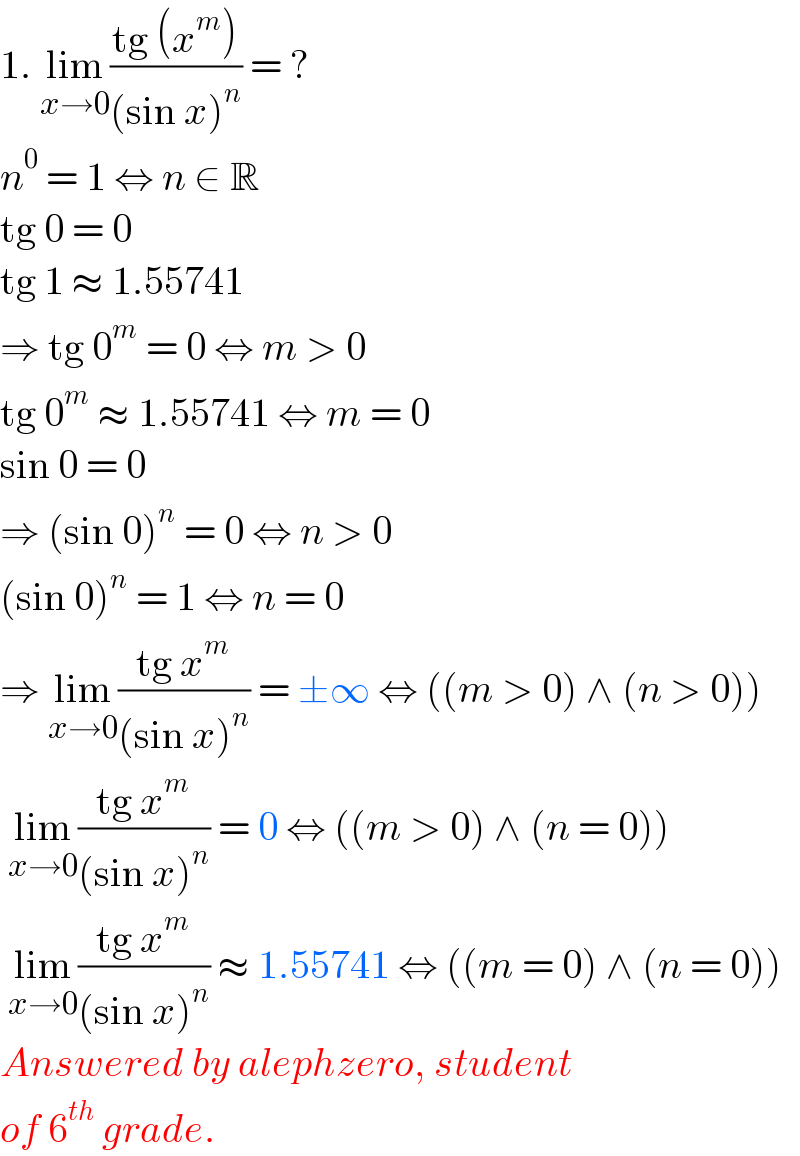
1. lim_(x→0) ((tg (x^m ))/((sin x)^n )) = ? n^0 = 1 ⇔ n ∈ R tg 0 = 0 tg 1 ≈ 1.55741 ⇒ tg 0^m = 0 ⇔ m > 0 tg 0^m ≈ 1.55741 ⇔ m = 0 sin 0 = 0 ⇒ (sin 0)^n = 0 ⇔ n > 0 (sin 0)^n = 1 ⇔ n = 0 ⇒ lim_(x→0) ((tg x^m )/((sin x)^n )) = ±∞ ⇔ ((m > 0) ∧ (n > 0)) lim_(x→0) ((tg x^m )/((sin x)^n )) = 0 ⇔ ((m > 0) ∧ (n = 0)) lim_(x→0) ((tg x^m )/((sin x)^n )) ≈ 1.55741 ⇔ ((m = 0) ∧ (n = 0)) Answered by alephzero, student of 6^(th) grade.
$$\mathrm{1}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tg}\:\left({x}^{{m}} \right)}{\left(\mathrm{sin}\:{x}\right)^{{n}} }\:=\:? \\ $$$${n}^{\mathrm{0}} \:=\:\mathrm{1}\:\Leftrightarrow\:{n}\:\in\:\mathbb{R} \\ $$$$\mathrm{tg}\:\mathrm{0}\:=\:\mathrm{0} \\ $$$$\mathrm{tg}\:\mathrm{1}\:\approx\:\mathrm{1}.\mathrm{55741} \\ $$$$\Rightarrow\:\mathrm{tg}\:\mathrm{0}^{{m}} \:=\:\mathrm{0}\:\Leftrightarrow\:{m}\:>\:\mathrm{0} \\ $$$$\mathrm{tg}\:\mathrm{0}^{{m}} \:\approx\:\mathrm{1}.\mathrm{55741}\:\Leftrightarrow\:{m}\:=\:\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{0}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{sin}\:\mathrm{0}\right)^{{n}} \:=\:\mathrm{0}\:\Leftrightarrow\:{n}\:>\:\mathrm{0} \\ $$$$\left(\mathrm{sin}\:\mathrm{0}\right)^{{n}} \:=\:\mathrm{1}\:\Leftrightarrow\:{n}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tg}\:{x}^{{m}} }{\left(\mathrm{sin}\:{x}\right)^{{n}} }\:=\:\pm\infty\:\Leftrightarrow\:\left(\left({m}\:>\:\mathrm{0}\right)\:\wedge\:\left({n}\:>\:\mathrm{0}\right)\right) \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tg}\:{x}^{{m}} }{\left(\mathrm{sin}\:{x}\right)^{{n}} }\:=\:\mathrm{0}\:\Leftrightarrow\:\left(\left({m}\:>\:\mathrm{0}\right)\:\wedge\:\left({n}\:=\:\mathrm{0}\right)\right) \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tg}\:{x}^{{m}} }{\left(\mathrm{sin}\:{x}\right)^{{n}} }\:\approx\:\mathrm{1}.\mathrm{55741}\:\Leftrightarrow\:\left(\left({m}\:=\:\mathrm{0}\right)\:\wedge\:\left({n}\:=\:\mathrm{0}\right)\right) \\ $$$${Answered}\:{by}\:{alephzero},\:{student} \\ $$$${of}\:\mathrm{6}^{{th}} \:{grade}. \\ $$
Commented by mr W last updated on 04/Dec/21
in this forum all members are equal. one doesn′t need to tell if he/she is teacher or student, old or young, man or woman, Indian or Japanese, buddist or muslim, earthling or marsian... only one thing is important: they love mathematics.
$${in}\:{this}\:{forum}\:{all}\:{members}\:{are}\:{equal}. \\ $$$${one}\:{doesn}'{t}\:{need}\:{to}\:{tell}\:{if}\:{he}/{she}\:{is}\: \\ $$$${teacher}\:{or}\:{student},\:{old}\:{or}\:{young},\:{man} \\ $$$${or}\:{woman},\:{Indian}\:{or}\:{Japanese},\: \\ $$$${buddist}\:{or}\:{muslim},\:{earthling}\:{or}\: \\ $$$${marsian}…\:{only}\:{one}\:{thing}\:{is}\: \\ $$$${important}:\:{they}\:\:{love}\:{mathematics}. \\ $$
Commented by greg_ed last updated on 05/Dec/21
right !
$$\mathrm{right}\:! \\ $$
Answered by mr W last updated on 04/Dec/21
(1) =lim_(x→0) ((tan (x^m ))/x^m )×((x/(sin x)))^n ×x^(m−n) =lim_(x→0) x^(m−n) = { ((1, if m=n)),((0, if m>n)),((∞, if m<n)) :} (2) =lim_(x→0) ((x(−2 sin^2 (x/2)))/((e^x −1)ln (1+3x^2 ))) =lim_(x→0) ((−2x sin^2 (x/2))/((x+(x^2 /(2!))+...)(3x^2 −((9x^4 )/2)+...))) =lim_(x→0) ((−2 sin^2 (x/2))/((1+(x/(2!))+...)(3−((9x^2 )/2)+...)x^2 )) =lim_(x→0) ((−1)/((1+(x/(2!))+...)(3−((9x^2 )/2)+...)×2))×(((sin (x/2))/(x/2)))^2 =−(1/(1×3×2))×1^2 =−(1/6)
$$\left(\mathrm{1}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left({x}^{{m}} \right)}{{x}^{{m}} }×\left(\frac{{x}}{\mathrm{sin}\:{x}}\right)^{{n}} ×{x}^{{m}−{n}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}^{{m}−{n}} =\begin{cases}{\mathrm{1},\:{if}\:{m}={n}}\\{\mathrm{0},\:{if}\:{m}>{n}}\\{\infty,\:{if}\:{m}<{n}}\end{cases} \\ $$$$\left(\mathrm{2}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\left(−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)}{\left({e}^{{x}} −\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} \right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}{x}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}{\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+…\right)\left(\mathrm{3}{x}^{\mathrm{2}} −\frac{\mathrm{9}{x}^{\mathrm{4}} }{\mathrm{2}}+…\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}{\left(\mathrm{1}+\frac{{x}}{\mathrm{2}!}+…\right)\left(\mathrm{3}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}+…\right){x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{1}}{\left(\mathrm{1}+\frac{{x}}{\mathrm{2}!}+…\right)\left(\mathrm{3}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}+…\right)×\mathrm{2}}×\left(\frac{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{1}×\mathrm{3}×\mathrm{2}}×\mathrm{1}^{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by Jamshidbek last updated on 05/Dec/21
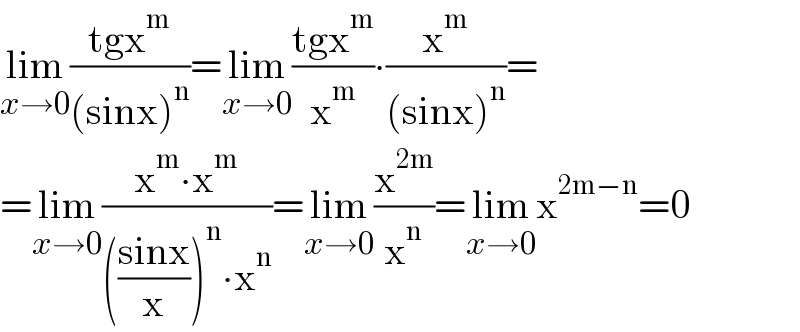
lim_(x→0) ((tgx^m )/((sinx)^n ))=lim_(x→0) ((tgx^m )/x^m )∙(x^m /((sinx)^n ))= =lim_(x→0) ((x^m ∙x^m )/((((sinx)/x))^n ∙x^n ))=lim_(x→0) (x^(2m) /x^n )=lim_(x→0) x^(2m−n) =0
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tgx}^{\mathrm{m}} }{\left(\mathrm{sinx}\right)^{\mathrm{n}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tgx}^{\mathrm{m}} }{\mathrm{x}^{\mathrm{m}} }\centerdot\frac{\mathrm{x}^{\mathrm{m}} }{\left(\mathrm{sinx}\right)^{\mathrm{n}} }= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{m}} \centerdot\mathrm{x}^{\mathrm{m}} }{\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\mathrm{n}} \centerdot\mathrm{x}^{\mathrm{n}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2m}} }{\mathrm{x}^{\mathrm{n}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}x}^{\mathrm{2m}−\mathrm{n}} =\mathrm{0} \\ $$
Commented by mr W last updated on 05/Dec/21
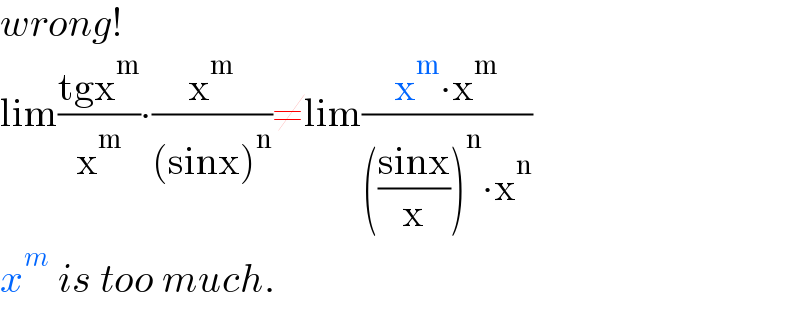
wrong! lim((tgx^m )/x^m )∙(x^m /((sinx)^n ))≠lim((x^m ∙x^m )/((((sinx)/x))^n ∙x^n )) x^m is too much.
$${wrong}! \\ $$$$\mathrm{lim}\frac{\mathrm{tgx}^{\mathrm{m}} }{\mathrm{x}^{\mathrm{m}} }\centerdot\frac{\mathrm{x}^{\mathrm{m}} }{\left(\mathrm{sinx}\right)^{\mathrm{n}} }\neq\mathrm{lim}\frac{\mathrm{x}^{\mathrm{m}} \centerdot\mathrm{x}^{\mathrm{m}} }{\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\mathrm{n}} \centerdot\mathrm{x}^{\mathrm{n}} } \\ $$$${x}^{{m}} \:{is}\:{too}\:{much}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *