Question Number 41761 by math khazana by abdo last updated on 12/Aug/18
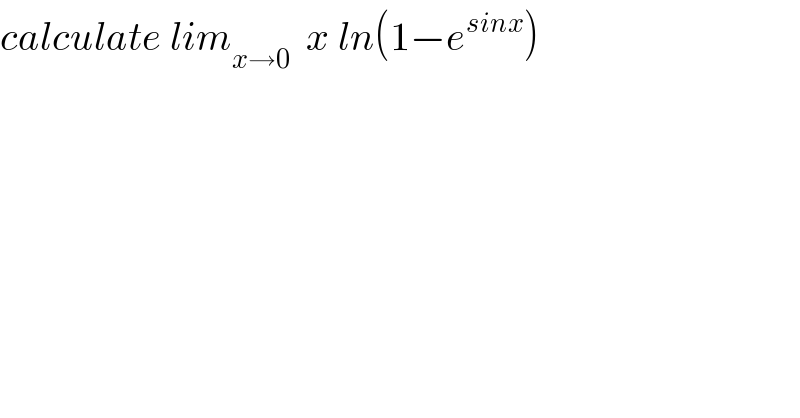
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:{x}\:{ln}\left(\mathrm{1}−{e}^{{sinx}} \right)\: \\ $$
Answered by alex041103 last updated on 12/Aug/18

$${As}\:{x}\rightarrow\mathrm{0}\:{the}\:{expression}\:{becomes}\:{one} \\ $$$${of}\:{the}\:{form}\:\mathrm{0}×\infty\:{which}\:{is}\:{easilu} \\ $$$${transformed}\:{in}\frac{\infty}{\infty}: \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}−{e}^{{sin}\:{x}} \right)}{\mathrm{1}/{x}}={L}'{Hopital} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−{e}^{{sinx}} {cosx}}{\mathrm{1}−{e}^{{sin}\:{x}} }}{−\mathrm{1}/{x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{e}^{{sin}\left({x}\right)} }{cosxe}^{{sinx}} = \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{e}^{{sinx}} }\mathrm{1} \\ $$$${Now}\:{we}\:{apply}\:{L}'{Hopital}\:{until}\:{we}\:{find} \\ $$$${a}\:{result}: \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{x}}{−{e}^{{sin}\left({x}\right)} {cos}\left({x}\right)}=\frac{\mathrm{2}×\mathrm{0}}{−{e}^{{sin}\left(\mathrm{0}\right)} {cos}\left(\mathrm{0}\right)}= \\ $$$$=\frac{\mathrm{0}}{\mathrm{1}×\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:{x}\:{ln}\left(\mathrm{1}−{e}^{{sinx}} \right)=\mathrm{0} \\ $$
