Question Number 48175 by Abdo msup. last updated on 20/Nov/18
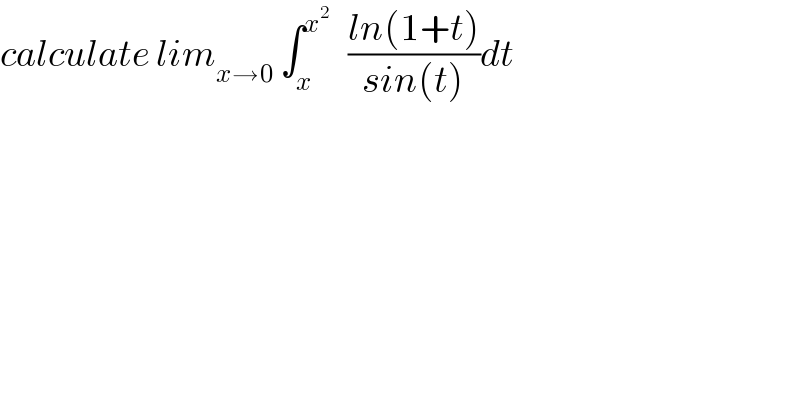
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\int_{{x}} ^{{x}^{\mathrm{2}} } \:\:\:\frac{{ln}\left(\mathrm{1}+{t}\right)}{{sin}\left({t}\right)}{dt} \\ $$
Commented by maxmathsup by imad last updated on 20/Nov/18
![∃ c ∈]x,x^2 [ /A(x)=∫_x ^x^2 ((ln(1+t))/(sin(t)))dt =(1/(sinc)) ∫_x ^x^2 ln(1+t)dt but ∫_x ^x^2 ln(1+t)dt =_(1+t=u) ∫_(1+x) ^(1+x^2 ) ln(u)du =[uln(u)−u]_(1+x) ^(1+x^2 ) =(1+x^2 )ln(1+x^2 )−(1+x^2 )−(1+x)ln(1+x)+1+x ∼(1+x^2 )x^2 +x−x^2 −x(1+x)=x^2 +x^4 −2x^2 =x^4 −x^2 x<c<x^2 ⇒∃α /c =αx +(1−α)x^2 and sinc∼c ⇒ ((x^4 −x^2 )/(αx (1−α)x^2 )) =((x^3 −x)/(α +(1−α)x)) →0 so lim_(x→0) A(x)=0](https://www.tinkutara.com/question/Q48199.png)
$$\left.\exists\:{c}\:\in\right]{x},{x}^{\mathrm{2}} \left[\:/{A}\left({x}\right)=\int_{{x}} ^{{x}^{\mathrm{2}} } \frac{{ln}\left(\mathrm{1}+{t}\right)}{{sin}\left({t}\right)}{dt}\:=\frac{\mathrm{1}}{{sinc}}\:\int_{{x}} ^{{x}^{\mathrm{2}} } \:{ln}\left(\mathrm{1}+{t}\right){dt}\:\:{but}\right. \\ $$$$\int_{{x}} ^{{x}^{\mathrm{2}} } {ln}\left(\mathrm{1}+{t}\right){dt}\:=_{\mathrm{1}+{t}={u}} \:\:\int_{\mathrm{1}+{x}} ^{\mathrm{1}+{x}^{\mathrm{2}} } {ln}\left({u}\right){du}\:=\left[{uln}\left({u}\right)−{u}\right]_{\mathrm{1}+{x}} ^{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}+{x}\right)+\mathrm{1}+{x} \\ $$$$\sim\left(\mathrm{1}+{x}^{\mathrm{2}} \right){x}^{\mathrm{2}} +{x}−{x}^{\mathrm{2}} \:−{x}\left(\mathrm{1}+{x}\right)={x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} ={x}^{\mathrm{4}} −{x}^{\mathrm{2}} \: \\ $$$${x}<{c}<{x}^{\mathrm{2}} \:\Rightarrow\exists\alpha\:/{c}\:=\alpha{x}\:+\left(\mathrm{1}−\alpha\right){x}^{\mathrm{2}} \:\:{and}\:{sinc}\sim{c}\:\Rightarrow \\ $$$$\frac{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} }{\alpha{x}\:\left(\mathrm{1}−\alpha\right){x}^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{3}} −{x}}{\alpha\:+\left(\mathrm{1}−\alpha\right){x}}\:\rightarrow\mathrm{0}\:{so}\:{lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right)=\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 20/Nov/18
![α∈]0,1[ .](https://www.tinkutara.com/question/Q48200.png)
$$\left.\alpha\in\right]\mathrm{0},\mathrm{1}\left[\:.\right. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Nov/18

$${I}=\int_{{x}} ^{{x}^{\mathrm{2}} } \frac{{ln}\left(\mathrm{1}+{t}\right)}{{sint}}{dt} \\ $$$$\frac{{dI}}{{dx}}=\int_{{x}} ^{{x}^{\mathrm{2}} } \frac{\partial}{\partial{x}}\left(\frac{{ln}\left(\mathrm{1}+{t}\right)}{{sint}}\right){dt}\:+\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{sinx}^{\mathrm{2}} }×\frac{{dx}^{\mathrm{2}} }{{dx}}−\frac{{ln}\left(\mathrm{1}+{x}\right)}{{sinx}}×\frac{{dx}}{{dx}} \\ $$$$=\mathrm{2}{x}×\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{sinx}^{\mathrm{2}} }−\frac{{ln}\left(\mathrm{1}+{x}\right)}{{sinx}} \\ $$$$=\mathrm{2}{x}×\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\frac{{sinx}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}−\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}×\frac{\mathrm{1}}{\frac{{sinx}}{{x}}} \\ $$$${when}\:{x}\rightarrow\mathrm{0} \\ $$$$=\mathrm{2}×\mathrm{0}×\frac{\mathrm{1}}{\mathrm{1}}−\mathrm{1}=−\frac{{dI}}{{dx}} \\ $$$$\frac{{dI}}{{dx}}=−\mathrm{1}\:\:\:{I}=−{x}+{c} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Nov/18

$${pls}\:{check}\:{sir}\:… \\ $$
