Question Number 166801 by mathocean1 last updated on 28/Feb/22
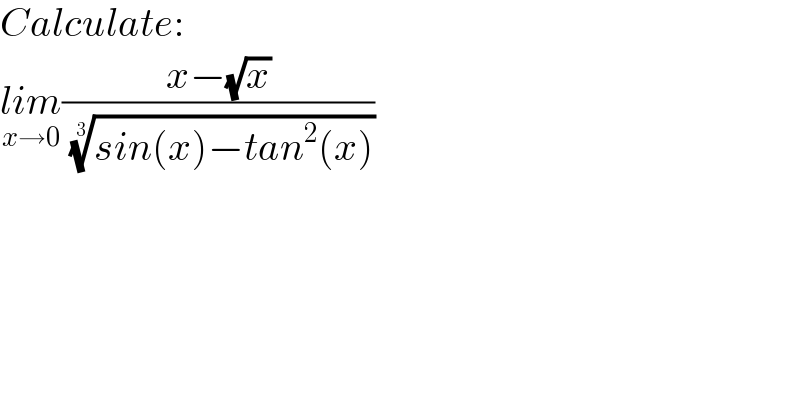
$${Calculate}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{x}−\sqrt{{x}}}{\:\sqrt[{\mathrm{3}}]{{sin}\left({x}\right)−{tan}^{\mathrm{2}} \left({x}\right)}} \\ $$
Commented by cortano1 last updated on 28/Feb/22
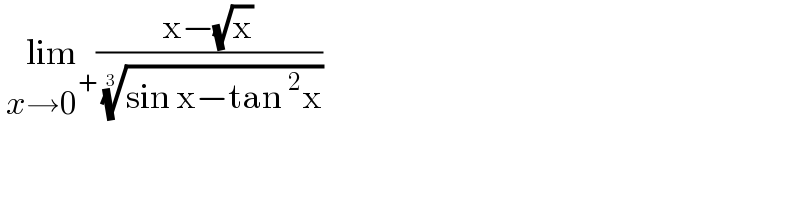
$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}−\sqrt{\mathrm{x}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{sin}\:\mathrm{x}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}} \\ $$
Commented by mathocean1 last updated on 28/Feb/22

$${yeah} \\ $$
Answered by bobhans last updated on 28/Feb/22
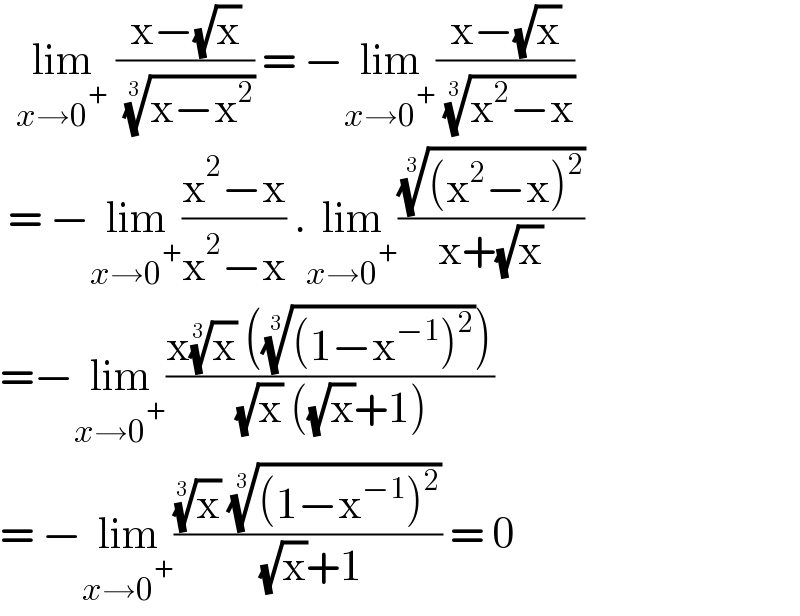
$$\:\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{x}−\sqrt{\mathrm{x}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{x}^{\mathrm{2}} }}\:=\:−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}−\sqrt{\mathrm{x}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}} \\ $$$$\:=\:−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\:.\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)^{\mathrm{2}} }}{\mathrm{x}+\sqrt{\mathrm{x}}} \\ $$$$=−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}\sqrt[{\mathrm{3}}]{\mathrm{x}}\:\left(\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{2}} }\right)}{\:\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)} \\ $$$$=\:−\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{x}}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{x}}+\mathrm{1}}\:=\:\mathrm{0} \\ $$
