Question Number 39635 by math khazana by abdo last updated on 09/Jul/18

$${calculate}\:\:{lim}_{{x}\rightarrow\mathrm{1}} \:\frac{\mathrm{1}+{cos}\left(\pi{x}\right)}{{x}^{\mathrm{2}} −\:{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)} \\ $$
Commented by abdo mathsup 649 cc last updated on 09/Jul/18

$${changement}\:\:{x}−\mathrm{1}={t}\:{give}\:{t}\rightarrow\mathrm{0}\:{whenx}\rightarrow\mathrm{1}\:{and} \\ $$$$\frac{\mathrm{1}+{cos}\left(\pi{x}\right)}{{x}^{\mathrm{2}} −{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}+{cos}\left(\pi\left(\mathrm{1}+{t}\right)\right)}{\left(\mathrm{1}+{t}^{} \right)^{\mathrm{2}} \:−{sin}\left(\frac{\pi\left(\mathrm{1}+{t}\right)}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}−{cost}}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:\:−{cos}\left(\frac{\pi{t}}{\mathrm{2}}\right)}={A}\left({t}\right)\:{but} \\ $$$$\mathrm{1}−{cost}\:\sim\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\:{and}\:\mathrm{1}−{cos}\left(\frac{\pi{t}}{\mathrm{2}}\right)\:\sim\:\frac{\pi^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{8}}\:\left({t}\rightarrow\mathrm{0}\right)\Rightarrow \\ $$$${A}\left({t}\right)\:\sim\frac{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\frac{\pi^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{8}}}\:=\:\:\frac{{t}}{\mathrm{2}\left({t}+\mathrm{2}\:+\frac{\pi^{\mathrm{2}} {t}}{\mathrm{8}}\right)}\:_{{t}\rightarrow\mathrm{0}} \rightarrow\mathrm{0} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\frac{\mathrm{1}+{cos}\left(\pi{x}\right)}{{x}^{\mathrm{2}} \:−{sin}\left(\frac{\pi{x}}{\mathrm{2}}\right)}\:=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Jul/18
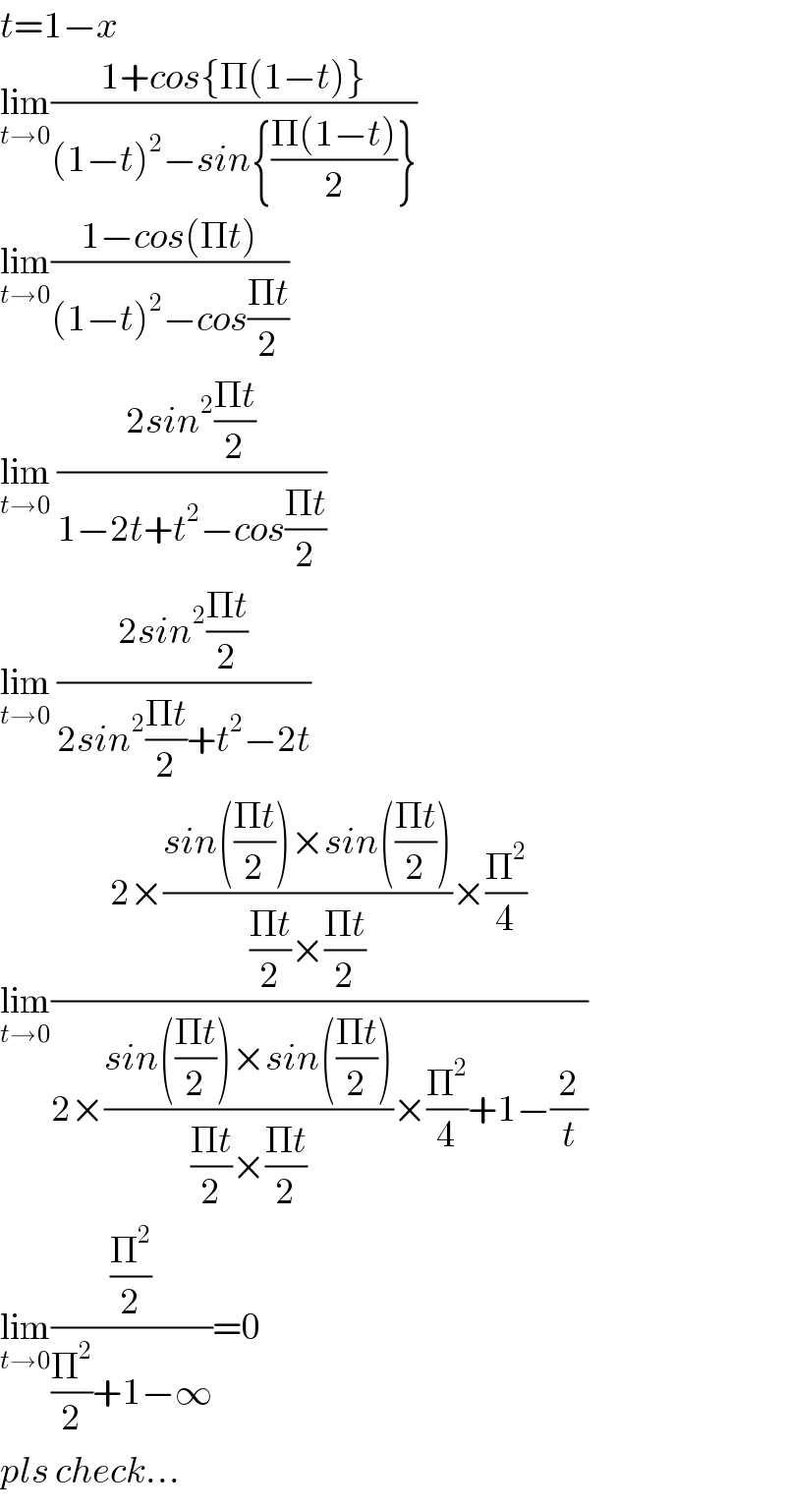
$${t}=\mathrm{1}−{x} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+{cos}\left\{\Pi\left(\mathrm{1}−{t}\right)\right\}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} −{sin}\left\{\frac{\Pi\left(\mathrm{1}−{t}\right)}{\mathrm{2}}\right\}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{cos}\left(\Pi{t}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} −{cos}\frac{\Pi{t}}{\mathrm{2}}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\Pi{t}}{\mathrm{2}}}{\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} −{cos}\frac{\Pi{t}}{\mathrm{2}}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\Pi{t}}{\mathrm{2}}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{\Pi{t}}{\mathrm{2}}+{t}^{\mathrm{2}} −\mathrm{2}{t}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}×\frac{{sin}\left(\frac{\Pi{t}}{\mathrm{2}}\right)×{sin}\left(\frac{\Pi{t}}{\mathrm{2}}\right)}{\frac{\Pi{t}}{\mathrm{2}}×\frac{\Pi{t}}{\mathrm{2}}}×\frac{\prod^{\mathrm{2}} }{\mathrm{4}}}{\mathrm{2}×\frac{{sin}\left(\frac{\Pi{t}}{\mathrm{2}}\right)×{sin}\left(\frac{\Pi{t}}{\mathrm{2}}\right)}{\frac{\Pi{t}}{\mathrm{2}}×\frac{\Pi{t}}{\mathrm{2}}}×\frac{\prod^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{2}}{{t}}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\prod^{\mathrm{2}} }{\mathrm{2}}}{\frac{\prod^{\mathrm{2}} }{\mathrm{2}}+\mathrm{1}−\infty}=\mathrm{0} \\ $$$${pls}\:{check}… \\ $$
