Question Number 87462 by mathocean1 last updated on 04/Apr/20
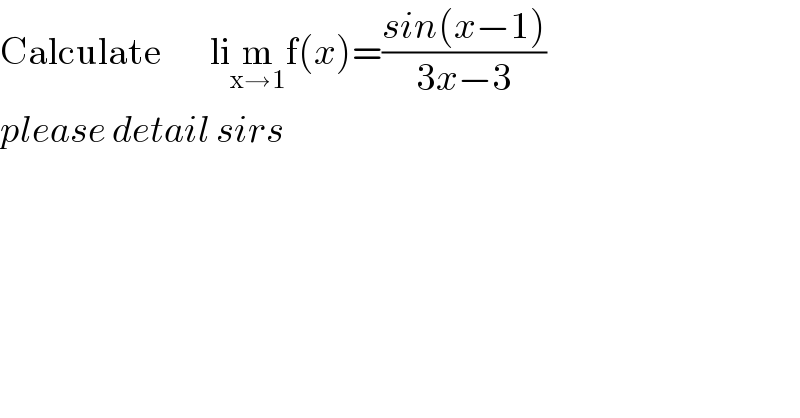
$$\mathrm{Calculate}\:\:\:\:\:\:\:\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{m}f}\left({x}\right)=\frac{{sin}\left({x}−\mathrm{1}\right)}{\mathrm{3}{x}−\mathrm{3}} \\ $$$${please}\:{detail}\:{sirs} \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{3x}−\mathrm{3}}\:? \\ $$
Commented by mathocean1 last updated on 04/Apr/20

$$\mathrm{yes} \\ $$
Commented by john santu last updated on 04/Apr/20
![lim_(x→1) ((sin (x−1))/(3(x−1))) , [ x−1=t ] lim_(t→0) ((sin t)/(3t)) = (1/3)](https://www.tinkutara.com/question/Q87471.png)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)}\:,\:\left[\:\mathrm{x}−\mathrm{1}=\mathrm{t}\:\right]\: \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{t}}{\mathrm{3t}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mathocean1 last updated on 04/Apr/20

$$\mathrm{great}\:\mathrm{sir}. \\ $$
Commented by mathocean1 last updated on 04/Apr/20

$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{do}\:\mathrm{to}\:\mathrm{write}\:\mathrm{correctly}\: \\ $$$$\mathrm{li}\underset{\mathrm{t}\rightarrow\mathrm{1}\:} {\mathrm{m}}\:…\:\mathrm{there}\:\mathrm{is}\:\mathrm{space}\:\mathrm{betwen}\:\mathrm{mine}… \\ $$
Commented by Ar Brandon last updated on 04/Apr/20

$${first}\:{write}\:{the}\:{text}\:{then}\:{you}\:{click} \\ $$$${on}\:{SEL}\:{to}\:{select}\:{the}\:{text}\:{then} \\ $$$${proceed}\:{as}\:{though}\:{it}'{s}\:{single}. \\ $$
Commented by $@ty@m123 last updated on 04/Apr/20