Question Number 79756 by mathmax by abdo last updated on 27/Jan/20
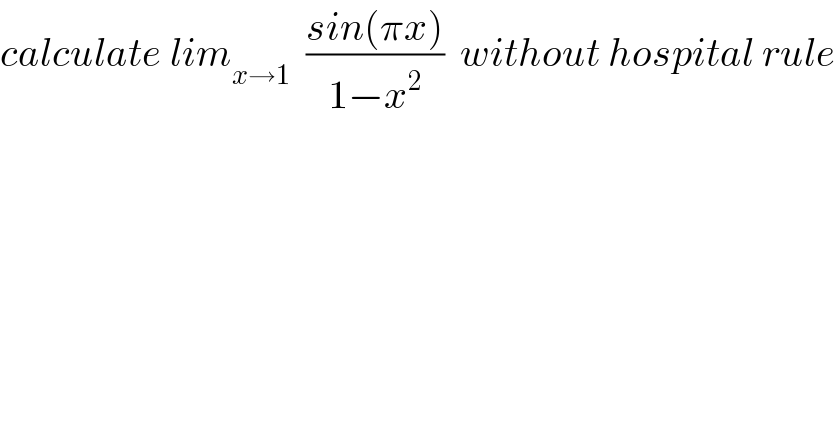
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{sin}\left(\pi{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:{without}\:{hospital}\:{rule} \\ $$
Commented by john santu last updated on 27/Jan/20

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\left(\pi−\pi\mathrm{x}\right)}{\left(\pi−\pi\mathrm{x}\right)}\right)×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\pi−\pi\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$=\:\mathrm{1}×\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\pi\left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)} \\ $$$$=\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 28/Jan/20

$${changement}\:\mathrm{1}−{x}={t}\:{give}\: \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\frac{{sin}\left(\pi{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left(\pi\left(\mathrm{1}−{t}\right)\right)}{\mathrm{1}−\left(\mathrm{1}−{t}\right)^{\mathrm{2}} } \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left(\pi{t}\right)}{\mathrm{1}−\left({t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{1}\right)}\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left(\pi{t}\right)}{\mathrm{2}{t}−{t}^{\mathrm{2}} } \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left(\pi{t}\right)}{\pi{t}}×\frac{\pi{t}}{\mathrm{2}{t}−{t}^{\mathrm{2}} }\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{{sin}\left(\pi{t}\right)}{\pi{t}}×{lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{\pi}{\mathrm{2}−{t}} \\ $$$$=\mathrm{1}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}} \\ $$
