Question Number 121010 by mathocean1 last updated on 04/Nov/20

$$\mathrm{calculate}: \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\:\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{x}+\mathrm{6}}} \\ $$
Answered by 675480065 last updated on 04/Nov/20
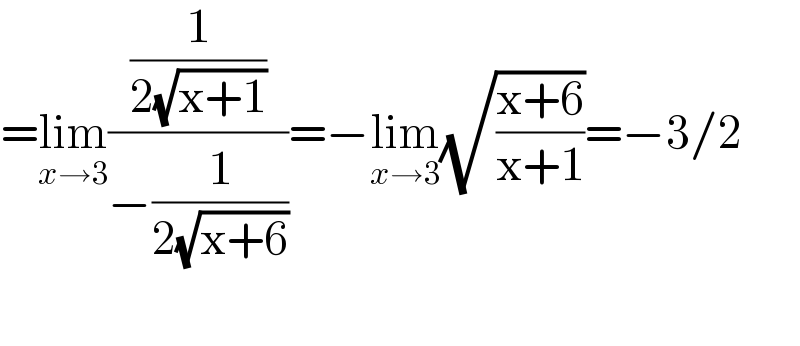
$$=\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}}{−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{6}}}}=−\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\sqrt{\frac{\mathrm{x}+\mathrm{6}}{\mathrm{x}+\mathrm{1}}}=−\mathrm{3}/\mathrm{2} \\ $$$$ \\ $$
Commented by mathocean1 last updated on 04/Nov/20

$$\mathrm{please}\:\mathrm{sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{detail}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{expression} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
Since on evaluating we get 0/0 we can therefore apply l'hôpital's rule by differentiating the numerator and the denominator.
Answered by Ar Brandon last updated on 04/Nov/20
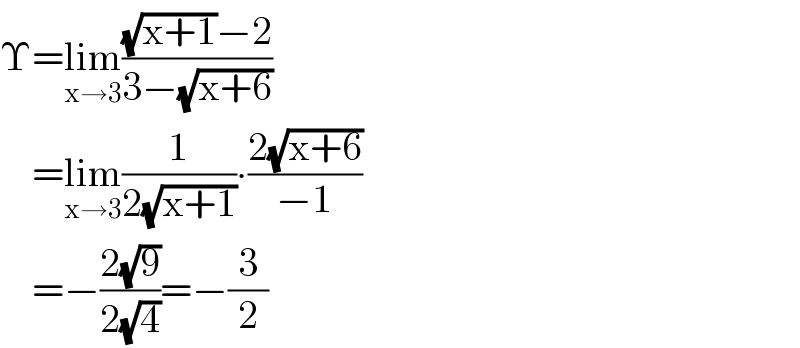
$$\Upsilon=\underset{\mathrm{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{x}+\mathrm{6}}} \\ $$$$\:\:\:\:=\underset{\mathrm{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}\centerdot\frac{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{6}}}{−\mathrm{1}} \\ $$$$\:\:\:\:=−\frac{\mathrm{2}\sqrt{\mathrm{9}}}{\mathrm{2}\sqrt{\mathrm{4}}}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 04/Nov/20
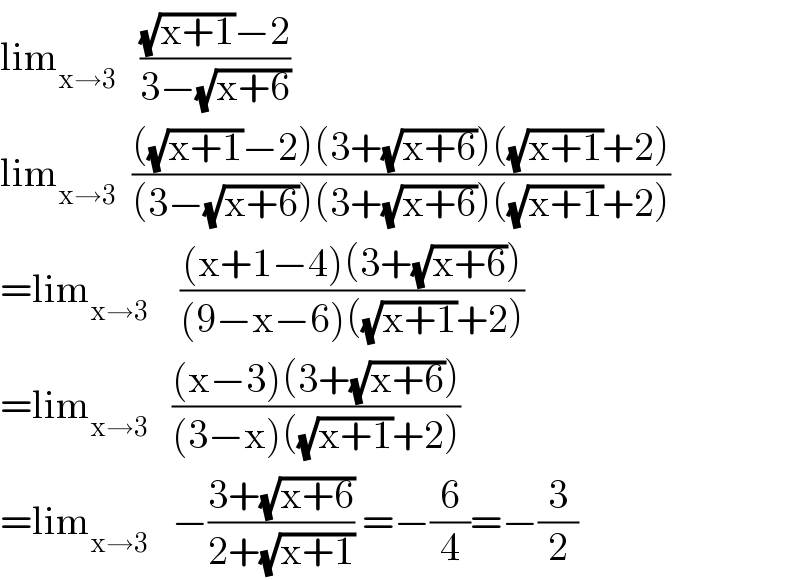
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \:\:\:\frac{\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{x}+\mathrm{6}}}\: \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \:\:\frac{\left(\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{2}\right)\left(\mathrm{3}+\sqrt{\mathrm{x}+\mathrm{6}}\right)\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)}{\left(\mathrm{3}−\sqrt{\mathrm{x}+\mathrm{6}}\right)\left(\mathrm{3}+\sqrt{\mathrm{x}+\mathrm{6}}\right)\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \:\:\:\:\frac{\left(\mathrm{x}+\mathrm{1}−\mathrm{4}\right)\left(\mathrm{3}+\sqrt{\mathrm{x}+\mathrm{6}}\right)}{\left(\mathrm{9}−\mathrm{x}−\mathrm{6}\right)\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \:\:\:\frac{\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{3}+\sqrt{\mathrm{x}+\mathrm{6}}\right)}{\left(\mathrm{3}−\mathrm{x}\right)\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \:\:\:−\frac{\mathrm{3}+\sqrt{\mathrm{x}+\mathrm{6}}}{\mathrm{2}+\sqrt{\mathrm{x}+\mathrm{1}}}\:=−\frac{\mathrm{6}}{\mathrm{4}}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
