Menu Close

Calculate-lim-x-x-3-3x-2-1-3-x-2-2x-lim-x-7-x-2-x-20-1-3-x-9-1-4-2-

Tinku Tara 0 Comments
Pin




Question Number 162672 by LEKOUMA last updated on 31/Dec/21
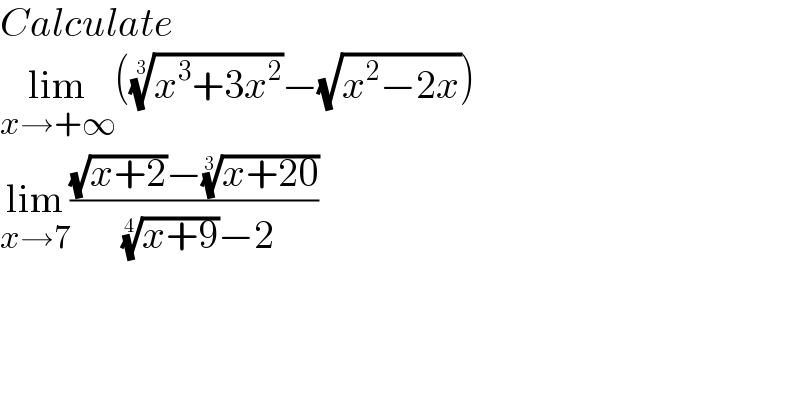
Calculate lim_(x→+∞) (((x^3 +3x^2 ))^(1/3) −(√(x^2 −2x))) lim_(x→7) (((√(x+2))−((x+20))^(1/3) )/( ((x+9))^(1/4) −2))
$${Calculate} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} }−\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\frac{\sqrt{{x}+\mathrm{2}}−\sqrt[{\mathrm{3}}]{{x}+\mathrm{20}}}{\:\sqrt[{\mathrm{4}}]{{x}+\mathrm{9}}−\mathrm{2}} \\ $$
Answered by tounghoungko last updated on 31/Dec/21
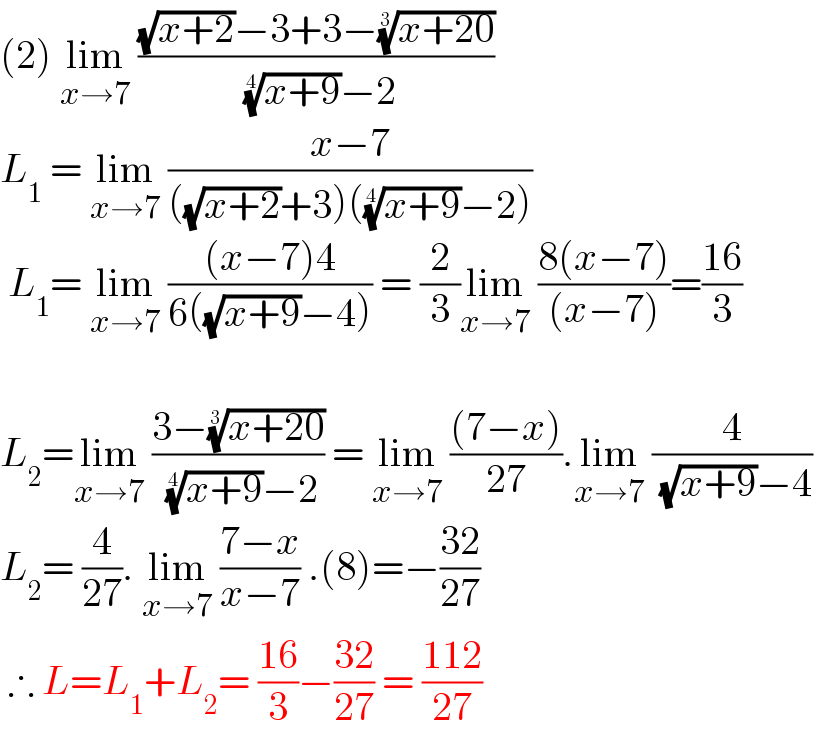
(2) lim_(x→7) (((√(x+2))−3+3−((x+20))^(1/3) )/( ((x+9))^(1/4) −2)) L_1 = lim_(x→7) ((x−7)/(((√(x+2))+3)(((x+9))^(1/4) −2))) L_1 = lim_(x→7) (((x−7)4)/(6((√(x+9))−4))) = (2/3)lim_(x→7) ((8(x−7))/((x−7)))=((16)/3) L_2 =lim_(x→7) ((3−((x+20))^(1/3) )/( ((x+9))^(1/4) −2)) = lim_(x→7) (((7−x))/(27)).lim_(x→7) (4/( (√(x+9))−4)) L_2 = (4/(27)). lim_(x→7) ((7−x)/(x−7)) .(8)=−((32)/(27)) ∴ L=L_1 +L_2 = ((16)/3)−((32)/(27)) = ((112)/(27))
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\sqrt{{x}+\mathrm{2}}−\mathrm{3}+\mathrm{3}−\sqrt[{\mathrm{3}}]{{x}+\mathrm{20}}}{\:\sqrt[{\mathrm{4}}]{{x}+\mathrm{9}}−\mathrm{2}} \\ $$$${L}_{\mathrm{1}} \:=\:\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{{x}−\mathrm{7}}{\left(\sqrt{{x}+\mathrm{2}}+\mathrm{3}\right)\left(\sqrt[{\mathrm{4}}]{{x}+\mathrm{9}}−\mathrm{2}\right)} \\ $$$$\:{L}_{\mathrm{1}} =\:\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{7}\right)\mathrm{4}}{\mathrm{6}\left(\sqrt{{x}+\mathrm{9}}−\mathrm{4}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\mathrm{8}\left({x}−\mathrm{7}\right)}{\left({x}−\mathrm{7}\right)}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$$$ \\ $$$${L}_{\mathrm{2}} =\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\mathrm{3}−\sqrt[{\mathrm{3}}]{{x}+\mathrm{20}}}{\:\sqrt[{\mathrm{4}}]{{x}+\mathrm{9}}−\mathrm{2}}\:=\:\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\left(\mathrm{7}−{x}\right)}{\mathrm{27}}.\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\mathrm{4}}{\:\sqrt{{x}+\mathrm{9}}−\mathrm{4}} \\ $$$${L}_{\mathrm{2}} =\:\frac{\mathrm{4}}{\mathrm{27}}.\:\underset{{x}\rightarrow\mathrm{7}} {\mathrm{lim}}\:\frac{\mathrm{7}−{x}}{{x}−\mathrm{7}}\:.\left(\mathrm{8}\right)=−\frac{\mathrm{32}}{\mathrm{27}} \\ $$$$\:\therefore\:{L}={L}_{\mathrm{1}} +{L}_{\mathrm{2}} =\:\frac{\mathrm{16}}{\mathrm{3}}−\frac{\mathrm{32}}{\mathrm{27}}\:=\:\frac{\mathrm{112}}{\mathrm{27}}\: \\ $$
Commented by LEKOUMA last updated on 31/Dec/21
Thank
$${Thank} \\ $$
Answered by tounghoungko last updated on 31/Dec/21
(1) lim_(x→∞) x ((1+(3/x)))^(1/3) −x (√(1−(2/x))) [ (1/x)=y ] L= lim_(y→0) ((((1+3y))^(1/3) −(√(1−2y)))/y) L= lim_(y→0) (((1+((3y)/3))−(1−((2y)/2)))/y) = 2
$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\:\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{3}}{{x}}}−{x}\:\sqrt{\mathrm{1}−\frac{\mathrm{2}}{{x}}}\: \\ $$$$\:\left[\:\frac{\mathrm{1}}{{x}}={y}\:\right]\: \\ $$$$\:{L}=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3}{y}}−\sqrt{\mathrm{1}−\mathrm{2}{y}}}{{y}}\: \\ $$$$\:{L}=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{3}{y}}{\mathrm{3}}\right)−\left(\mathrm{1}−\frac{\mathrm{2}{y}}{\mathrm{2}}\right)}{{y}}\:=\:\mathrm{2} \\ $$
Commented by LEKOUMA last updated on 31/Dec/21
Thank
$${Thank} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *