Question Number 42779 by maxmathsup by imad last updated on 02/Sep/18
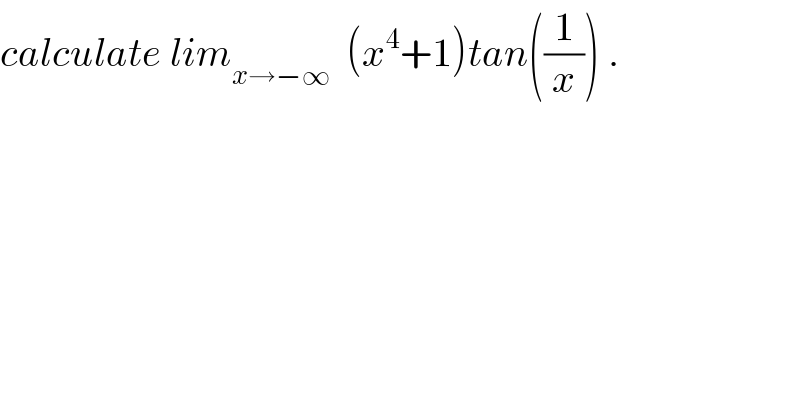
$${calculate}\:{lim}_{{x}\rightarrow−\infty} \:\:\left({x}^{\mathrm{4}} +\mathrm{1}\right){tan}\left(\frac{\mathrm{1}}{{x}}\right)\:. \\ $$
Commented by maxmathsup by imad last updated on 06/Nov/18
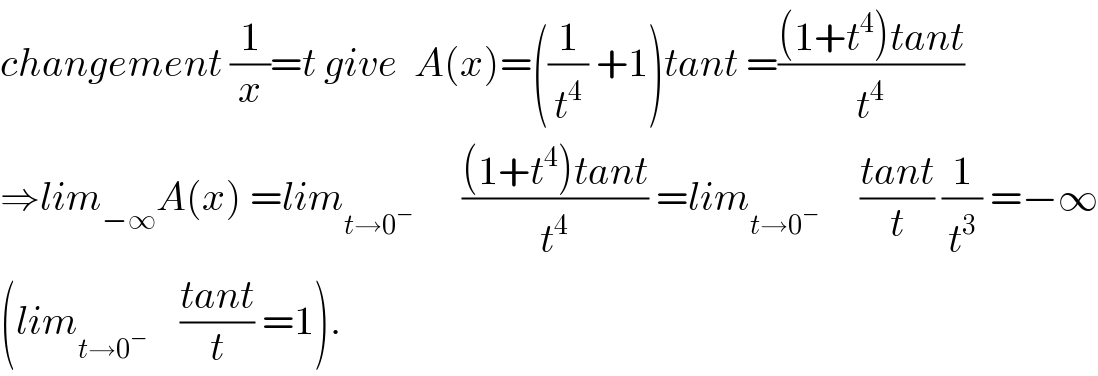
$${changement}\:\frac{\mathrm{1}}{{x}}={t}\:{give}\:\:{A}\left({x}\right)=\left(\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\:+\mathrm{1}\right){tant}\:=\frac{\left(\mathrm{1}+{t}^{\mathrm{4}} \right){tant}}{{t}^{\mathrm{4}} } \\ $$$$\Rightarrow{lim}_{−\infty} {A}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{0}^{−} } \:\:\:\:\:\:\frac{\left(\mathrm{1}+{t}^{\mathrm{4}} \right){tant}}{{t}^{\mathrm{4}} }\:={lim}_{{t}\rightarrow\mathrm{0}^{−} } \:\:\:\:\:\frac{{tant}}{{t}}\:\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:=−\infty \\ $$$$\left({lim}_{{t}\rightarrow\mathrm{0}^{−} } \:\:\:\:\frac{{tant}}{{t}}\:=\mathrm{1}\right). \\ $$
