Question Number 42392 by abdo.msup.com last updated on 24/Aug/18
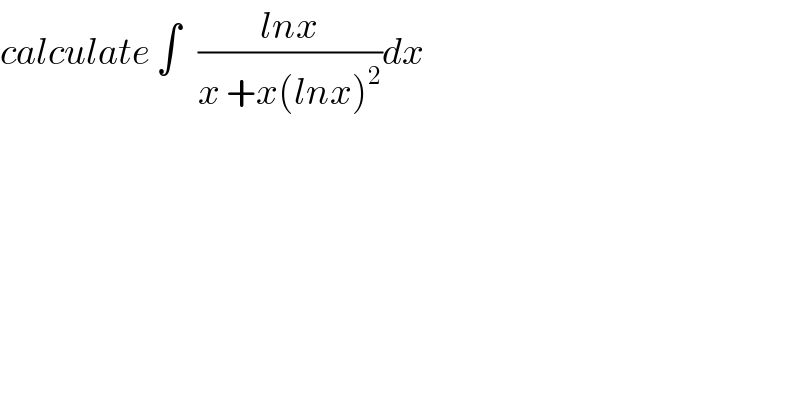
$${calculate}\:\int\:\:\:\frac{{lnx}}{{x}\:+{x}\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by maxmathsup by imad last updated on 25/Aug/18
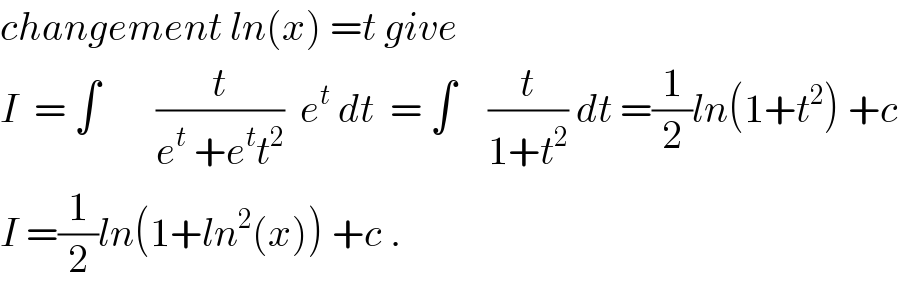
$${changement}\:{ln}\left({x}\right)\:={t}\:{give}\: \\ $$$${I}\:\:=\:\int\:\:\:\:\:\:\:\frac{{t}}{{e}^{{t}} \:+{e}^{{t}} {t}^{\mathrm{2}} }\:\:{e}^{{t}} \:{dt}\:\:=\:\int\:\:\:\:\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:+{c} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{ln}^{\mathrm{2}} \left({x}\right)\right)\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18
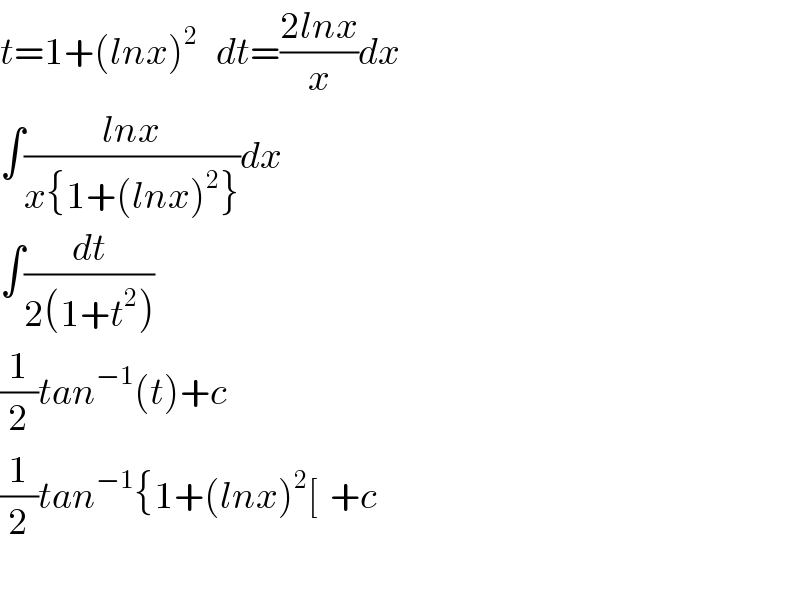
$${t}=\mathrm{1}+\left({lnx}\right)^{\mathrm{2}} \:\:\:{d}\overset{} {{t}}=\frac{\mathrm{2}{lnx}}{{x}}{dx} \\ $$$$\int\frac{{lnx}}{{x}\left\{\mathrm{1}+\left({lnx}\right)^{\mathrm{2}} \right\}}{dx} \\ $$$$\int\frac{{dt}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left({t}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left\{\mathrm{1}+\left({lnx}\right)^{\mathrm{2}} \left[\:\:+{c}\right.\right. \\ $$$$ \\ $$
