Question Number 62879 by mathmax by abdo last updated on 26/Jun/19
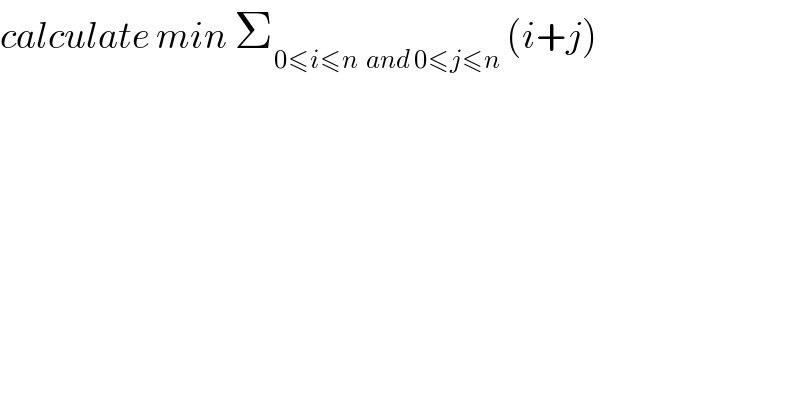
$${calculate}\:{min}\:\sum_{\mathrm{0}\leqslant{i}\leqslant{n}\:\:{and}\:\mathrm{0}\leqslant{j}\leqslant{n}} \:\left({i}+{j}\right) \\ $$
Answered by mr W last updated on 26/Jun/19
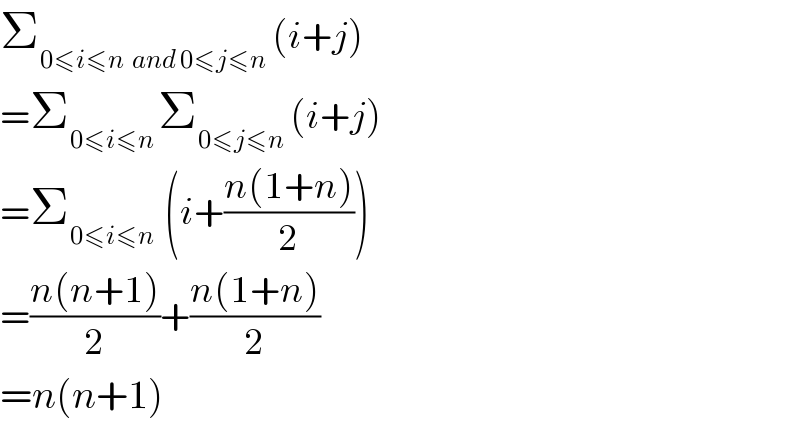
$$\sum_{\mathrm{0}\leqslant{i}\leqslant{n}\:\:{and}\:\mathrm{0}\leqslant{j}\leqslant{n}} \:\left({i}+{j}\right) \\ $$$$=\sum_{\mathrm{0}\leqslant{i}\leqslant{n}\:} \sum_{\mathrm{0}\leqslant{j}\leqslant{n}} \:\left({i}+{j}\right) \\ $$$$=\sum_{\mathrm{0}\leqslant{i}\leqslant{n}\:} \:\left({i}+\frac{{n}\left(\mathrm{1}+{n}\right)}{\mathrm{2}}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\frac{{n}\left(\mathrm{1}+{n}\right)}{\mathrm{2}} \\ $$$$={n}\left({n}+\mathrm{1}\right) \\ $$
