Question Number 157823 by mnjuly1970 last updated on 28/Oct/21
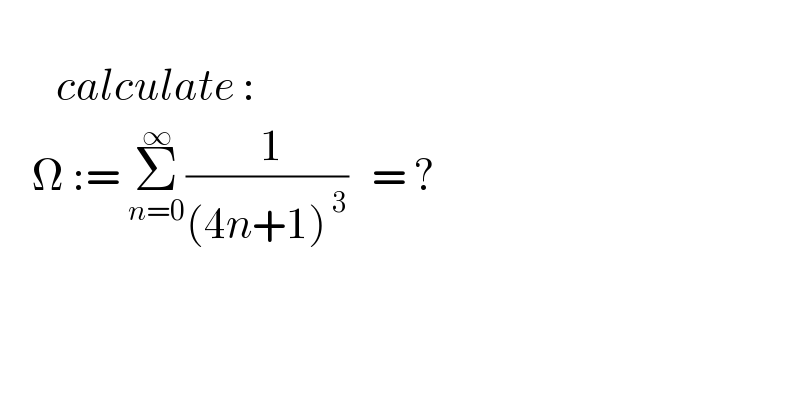
$$ \\ $$$$\:\:\:\:\:\:\:{calculate}\:: \\ $$$$\:\:\:\:\Omega\::=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\:\mathrm{1}}{\left(\mathrm{4}{n}+\mathrm{1}\right)^{\:\mathrm{3}} }\:\:\:=\:? \\ $$$$\: \\ $$
Answered by qaz last updated on 28/Oct/21
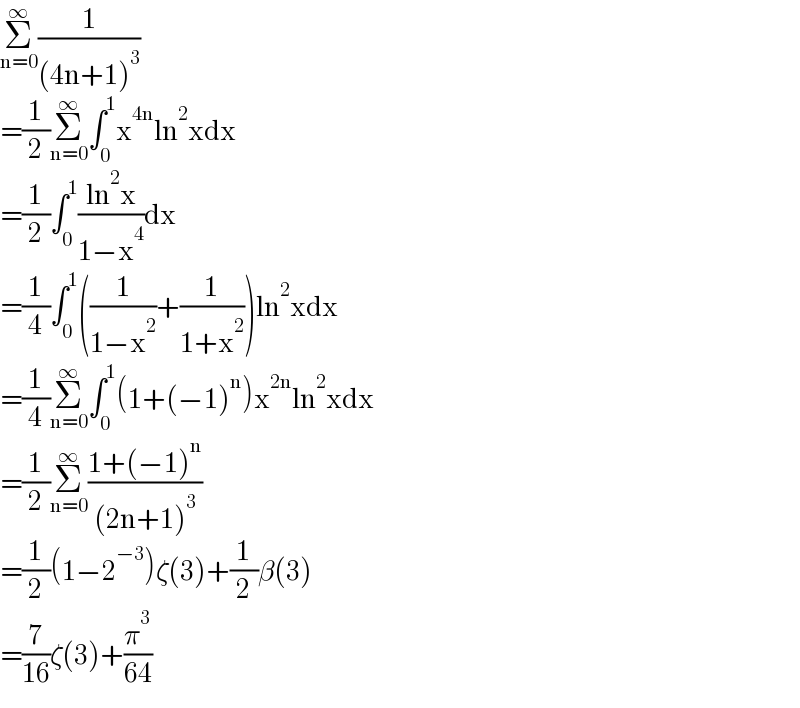
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{4n}} \mathrm{ln}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{ln}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{2n}} \mathrm{ln}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}^{−\mathrm{3}} \right)\zeta\left(\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\mathrm{3}\right) \\ $$$$=\frac{\mathrm{7}}{\mathrm{16}}\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{3}} }{\mathrm{64}} \\ $$
Commented by mnjuly1970 last updated on 28/Oct/21
$$\:{God}\:{bless}\:{you}\:{sir}\:{qaz}\:{very}\:{nice}\:{solution} \\ $$
