Question Number 56330 by maxmathsup by imad last updated on 14/Mar/19
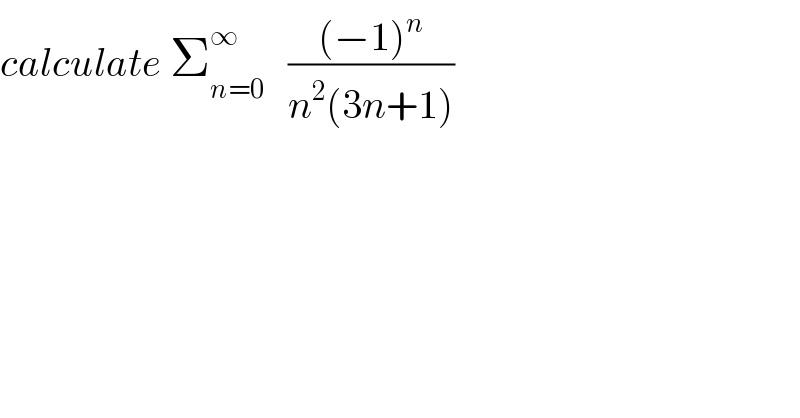
$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} \left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$
Commented by maxmathsup by imad last updated on 24/Mar/19
![let decompose F(x)=(1/(x^2 (3x+1))) ⇒F(x)=(a/x) +(b/x^2 ) +(c/(3x+1)) b=lim_(x→0) x^2 F(x)=1 c =lim_(x→−(1/3)) (3x+1)F(x) =9 ⇒F(x)=(a/x) +(1/x^2 ) +(9/(3x+1)) F(−1) =−(1/2) =−a +1 −(9/2) ⇒−1 =−2a +2 −9 ⇒−1=−2a−7 ⇒ 2a =−6 ⇒a =−3 ⇒F(x)=−(3/x) +(1/x^2 ) +(9/(3x+1)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) =−3 Σ_(n=1) ^∞ (((−1)^n )/n) +Σ_(n=1) ^∞ (((−1)^n )/n^2 ) +9 Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) but Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) let find Σ_(n=1) ^∞ (((−1)^n )/n^2 ) we have Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/(4n^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(3/4) (π^2 /6) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(π^2 /(24)) −(π^2 /8) =((π^2 −3π^2 )/(24)) =−(π^2 /(12)) let determine Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) let S(x) =Σ_(n=1) ^∞ (−1)^n (x^(3n+1) /(3n+1)) with ∣x∣<1 ⇒(dS/dx)(x) =Σ_(n=1) ^∞ (−1)^n x^(3n) =Σ_(n=1) ^∞ (−x^3 )^n =(1/(1+x^3 )) −1 =((−x^3 )/(1+x^3 )) ⇒S(x) =∫_0 ^x ((−t^3 )/(1+t^3 )) dt +λ S(0)=0 ⇒λ =0 ⇒ S(x) =−∫_0 ^x ((t^3 +1−1)/(t^3 +1)) dt =−x + ∫_0 ^x (dt/(t^3 +1)) let decompose F(t) =(1/(t^3 +1)) =(1/((t+1)(t^2 −t+1))) F(t)=(a/(t+1)) +((bt +c)/(t^2 −t +1)) a =lim_(t→−1) (t+1)F(t)=(1/3) lim_(t→+∞) t F(t) =0 =a+b ⇒b =−(1/3) ⇒F(t) =(1/(3(t+1))) −(1/3) ((t−3c)/(t^2 −t +1)) F(o) =1 =(1/3) +c ⇒c =(2/3) ⇒F(t)=(1/(3(t+1))) −(1/3) ((t−2)/(t^2 −t+1)) ⇒ ∫ F(t)dt =(1/3)ln∣t+1∣ −(1/6) ∫ ((2t−1−3)/(t^2 −t+1)) dt =(1/3)ln∣t+1∣−(1/6)ln(t^2 −t +1) +(1/2) ∫ (dt/(t^2 −t +1)) but ∫ (dt/(t^2 −t +1)) =∫ (dt/((t−(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du =(4/3) ((√3)/2) arctanu +c =(2/( (√3))) arctan(((2t+1)/( (√3)))) ⇒ S(x)=−x +[(1/3)ln∣t+1∣−(1/6)ln(t^2 −t+1)+(1/( (√3))) arctan(((2t+1)/( (√3))))]_0 ^x =−x +{(1/3)ln∣x+1∣−(1/6)ln(x^2 −x+1)+(1/( (√3))) arctan(((2x+1)/( (√3))))−(1/( (√3))) arctan((1/( (√3))))} ⇒ Σ_(n=1) ^∞ (((−1)^n )/(3n+1)) =S(1) =−1 +(1/3)ln(2) +(1/( (√3))) arctan((√3))−(1/( (√3))) arctan((1/( (√3)))) =−1 +(1/3)ln(2) +(1/( (√3))) arctan((√3))−(1/( (√3)))((π/2) −arctan((√3))) =−1 +((ln(2))/3) +(2/( (√3))) arctan((√3)) −(π/(2(√3))) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n^2 (3n+1))) = 3ln(2) −(π^2 /(12)) −9 +3ln(2) +((18)/( (√3))) arctan((√3)) −((9π)/(2(√3))) .](https://www.tinkutara.com/question/Q56814.png)
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{3}{x}+\mathrm{1}\right)}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{\mathrm{3}{x}+\mathrm{1}} \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{0}} {x}^{\mathrm{2}} \:{F}\left({x}\right)=\mathrm{1} \\ $$$${c}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{3}}} \:\:\:\left(\mathrm{3}{x}+\mathrm{1}\right){F}\left({x}\right)\:=\mathrm{9}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{9}}{\mathrm{3}{x}+\mathrm{1}} \\ $$$${F}\left(−\mathrm{1}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:=−{a}\:+\mathrm{1}\:−\frac{\mathrm{9}}{\mathrm{2}}\:\Rightarrow−\mathrm{1}\:=−\mathrm{2}{a}\:+\mathrm{2}\:−\mathrm{9}\:\Rightarrow−\mathrm{1}=−\mathrm{2}{a}−\mathrm{7}\:\Rightarrow \\ $$$$\mathrm{2}{a}\:=−\mathrm{6}\:\Rightarrow{a}\:=−\mathrm{3}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{3}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{9}}{\mathrm{3}{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} \left(\mathrm{3}{n}+\mathrm{1}\right)}\:=−\mathrm{3}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:+\mathrm{9}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{1}} \\ $$$${but}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}}\:=−\boldsymbol{{ln}}\left(\mathrm{2}\right)\:\:\boldsymbol{{let}}\:\boldsymbol{{find}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$$${we}\:{have}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\pi^{\mathrm{2}} −\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{24}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:\:{let}\:{determine}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{1}} \\ $$$${let}\:{S}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\:\:\frac{{x}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}}\:\:{with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow\frac{{dS}}{{dx}}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{\boldsymbol{{n}}} \:\boldsymbol{{x}}^{\mathrm{3}\boldsymbol{{n}}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\boldsymbol{{x}}^{\mathrm{3}} \right)^{\boldsymbol{{n}}} \:=\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{3}} }\:−\mathrm{1}\:\:=\frac{−\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{3}} }\:\Rightarrow{S}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{−{t}^{\mathrm{3}} }{\mathrm{1}+{t}^{\mathrm{3}} }\:{dt}\:+\lambda \\ $$$${S}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\lambda\:=\mathrm{0}\:\Rightarrow\:{S}\left({x}\right)\:=−\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}^{\mathrm{3}} +\mathrm{1}−\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:{dt} \\ $$$$=−{x}\:\:+\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{t}−\mathrm{3}{c}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}} \\ $$$${F}\left({o}\right)\:=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+{c}\:\Rightarrow{c}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{3}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{t}−\mathrm{2}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int\:\frac{\mathrm{2}{t}−\mathrm{1}−\mathrm{3}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} −{t}\:+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:{but} \\ $$$$\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:=\int\:\:\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\:\:\:\:\int\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{du} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{arctanu}\:+{c}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$${S}\left({x}\right)=−{x}\:\:\:+\left[\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{{x}} \\ $$$$=−{x}\:+\left\{\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{1}}\:={S}\left(\mathrm{1}\right)\:=−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\sqrt{\mathrm{3}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\sqrt{\mathrm{3}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\sqrt{\mathrm{3}}\right)\right) \\ $$$$=−\mathrm{1}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\sqrt{\mathrm{3}}\right)\:−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} \left(\mathrm{3}{n}+\mathrm{1}\right)}\:=\:\mathrm{3}{ln}\left(\mathrm{2}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:−\mathrm{9}\:+\mathrm{3}{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{18}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\sqrt{\mathrm{3}}\right)\:−\frac{\mathrm{9}\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:. \\ $$
